코드링크
캐니에지
1986년 캐니에 의해 설계된 에지 검출 연산자이다. 현재 가장 널리 사용되며 에지 검출을 최적화 문제로 취급했다.
다음은 캐니가 제시한 좋은 에지 알고리즘의 세가지 기준이다.
- 최소 오류율 : 거짓 긍정과 거짓 부정이 최소여야 한다. 즉, 없는 에지가 생성되거나 있는 에지를 못 찾는 경우를 최소로 유지해야 한다.
- 위치 정확도 : 검출된 에지는 실제 에지의 위치와 가급적 가까워야 한다.
- 에지 두께 : 실제 에지에 해당하는 곳에는 한 두께의 에지만 생성해야 한다.
하지만 위 조건을 모두 만족하는 일반적인 연산자를 찾아내는 것은 불가능한 일이다. 따라서 1차원 계단 에지에 화이트 잡음이 첨가된 상활을 가정해 최적화 작업을 했다. 그 결과 가우시안에 1차 미분을 적용한 연산자가 최적임을 수학적으로 증명했다.
하지만 1차원에서 도출된 결과를 2차원으로 확장하려면 gradient 방향을 찾아내 그 방향으로 미분을 해야 한다. 이 과정을 소벨이나 프레윗같은 마스크를 이용해 gradient 방향을 구하는 것으로 근사화할 수 있고, 이때 발생하는 오류는 허용할 수 있는 범위에 있다는 것도 증명했다.
이렇게 구한 에지 영상은 에지가 두껍기 때문에 얇게 바꾸는 비최대 억제라는 단계를 추가했다. 마지막으로 거짓 긍정 에지를 제거하는 이력 임계값 단계를 적용한다.
비최대 억제와 이력 임계값
비최대 억제(non-maximum suppression)은 자신의 이웃보다 크지 않은 화소를 에지가 아닌 것으로 결정한다. 각각의 이웃은 다음과 같다.
- 에지 방향 0 : 위,아래
- 에지 방향 1 : 북동,남서
- 에지 방향 2 : 왼쪽,오른쪽
- 에지 방향 3 : 북서, 남동
이 방식을 사용하면 에지가 아닌데 에지로 판정되는 거짓 긍정의 케이스가 생긴다. 가장 간단한 방법은 임계값을 설정해 임계값보다 낮은 값을 거짓으로 하는 것이다.
임계값을 한번만 설정하면 에지인데 에지가 아닌것으로 판단되는 거짓 부정의 케이스가 생길수도 있기 때문에 높은 임계값으로 걸러진 영상에서 각 이웃 픽셀을 2~3배 낮은 임계값으로 한번더 확인한다.
이렇게 두 개의 임계값을 쓰는 방식을 이력 임계값(Hysteresis thresholding) 방법이라고 한다.
코드 구현
다음의 사진으로 구현해본다.
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./data/food.jpg',cv2.IMREAD_GRAYSCALE)
plt.imshow(img,cmap='gray')
plt.show()

컨볼루션 연산은 지난번에 사용한 것과 동일하다.
def im2col(input_data, filter_h, filter_w):
H, W, C = input_data.shape
u_pad_h = (filter_h-1)//2
d_pad_h = (filter_h-1)//2
l_pad_w = (filter_w-1)//2
r_pad_w = (filter_w-1)//2
if (filter_h-1) %2 ==1:
u_pad_h +=1
if (filter_w-1)%2 ==1:
l_pad_w +=1
input_data = cv2.copyMakeBorder(input_data, u_pad_h, d_pad_h, l_pad_w, r_pad_w, cv2.BORDER_REPLICATE)
if C==1:
input_data= np.expand_dims(input_data,-1)
img = np.transpose(input_data,(2,0,1))
col = np.zeros(( C, filter_h, filter_w, H, W))
for y in range(filter_h):
y_max = y + H
for x in range(filter_w):
x_max = x + W
col[:, y, x, :, :] = img[:, y:y_max:1, x:x_max:1]
col = np.transpose(col,(0,3,4,1,2)).reshape(C*H*W, -1)
return col
def conv(img,filter):
filter_h ,filter_w = filter.shape
if len(img.shape) ==3:
img_h,img_w,c = img.shape
elif len(img.shape)==2:
img_h,img_w = img.shape
c=1
img = np.expand_dims(img,-1)
else:
print("Length of image shape must over 2")
return
col = im2col(img,filter_h,filter_w)
col_filetr = filter.reshape((1,-1)).T
out = np.dot(col, col_filetr)
return np.transpose(out.reshape((c, img_h, img_w)),(1, 2,0))
가우시안 필터를 만드는 연산 역시 지난번과 동일하다.
def gaussian2d(x,y,sigma):
x2 = x**2
y2 = y**2
sigma2 = sigma**2
return (1/(2*np.pi*sigma2))*np.exp(-1*((x2+y2)/(2*sigma2)))
def make_gaussian(sigma):
size = int(sigma * 6)
if size % 2 == 0:
size += 1
aran = np.arange(-1 * (size // 2), size // 2 + 1)
XX, YY = np.meshgrid(aran, aran)
return gaussian2d(XX, YY, sigma)
소벨 연산의 경우 에지 강도는 지난번과 동일하다. 다만 에지 방향을 저번에 구하지 않았었는데 arctan(dy_image,dx_image)를 하면 그레디언트의 방향을 알 수 있다. 그레디언트의 방향과 에지 방향은 서로 직교하므로 90을 더해주고 03과 47은 동일하므로 0이하의 값에 180을 더했다.
def direction_quantization(atan):
ret = np.where(np.logical_and(atan>=22.5,atan<67.5),7,4)
ret = np.where(np.logical_and(atan >= 67.5, atan < 111.5), 6, ret)
ret = np.where(np.logical_and(atan >= 111.5, atan < 157.5), 5, ret)
return ret
def sobel(img):
sobel_mask_y = np.array([[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]])
sobel_mask_x = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
dy_image = conv(img, sobel_mask_y).squeeze()
dx_image = conv(img, sobel_mask_x).squeeze()
dy_image[0, :] = dy_image[-1, :] = 0
dx_image[:, 0] = dx_image[:, -1] = 0
Sobel = np.uint8(np.sqrt((dy_image ** 2) + (dx_image ** 2)))
atan = np.arctan2(dy_image, dx_image) / np.pi * 180
atan += 90
atan[atan > 180] = 360 - atan[atan > 180]
atan[atan < 0] += 180
direc = direction_quantization(atan)
return Sobel, direc
소벨 필터를 거친 이미지에서 에지의 방향에 따라 각각의 이웃보다 큰지 확인하기 위해서 다음과 같이 함수를 작성했다.
def non_maximum_suppression(img,direction):
e_img = np.pad(img[:, 1:], ((0, 0), (0, 1)),constant_values=255)
w_img = np.pad(img[:, :-1], ((0, 0), (1, 0)),constant_values=255)
n_img = np.pad(img[:-1, :], ((1, 0), (0, 0)),constant_values=255)
s_img = np.pad(img[1:, :], ((0, 1), (0, 0)),constant_values=255)
se_img = np.pad(s_img[:, 1:], ((0, 0), (0, 1)),constant_values=255)
ne_img = np.pad(n_img[:, 1:], ((0, 0), (0, 1)),constant_values=255)
sw_img = np.pad(s_img[:, :-1], ((0, 0), (1, 0)),constant_values=255)
nw_img = np.pad(n_img[:, :-1], ((0, 0), (1, 0)),constant_values=255)
ret = np.where(direction == 4, np.logical_and(img >= n_img, img >= s_img), False)
ret = np.where(direction == 5, np.logical_and(img >= ne_img, img >= sw_img), ret)
ret = np.where(direction == 6, np.logical_and(img >= e_img, img >= w_img), ret)
ret = np.where(direction == 7, np.logical_and(img >= nw_img, img >= se_img), ret)
return ret
이제 케니연산자의 전체 함수는 다음과 같다.
def neighbor(img):
img = np.uint8(img)
e_img = np.pad(img[:, 1:], ((0, 0), (0, 1)))
w_img = np.pad(img[:, :-1], ((0, 0), (1, 0)))
n_img = np.pad(img[:-1, :], ((1, 0), (0, 0)))
s_img = np.pad(img[1:, :], ((0, 1), (0, 0)))
se_img = np.pad(s_img[:, 1:], ((0, 0), (0, 1)))
ne_img = np.pad(n_img[:, 1:], ((0, 0), (0, 1)))
sw_img = np.pad(s_img[:, :-1], ((0, 0), (1, 0)))
nw_img = np.pad(n_img[:, :-1], ((0, 0), (1, 0)))
return (w_img+e_img+n_img+s_img+sw_img+nw_img+se_img+ne_img+img)>0
def hysteresis_thresholding(img,th_low,th_high,direction):
non_maxim = np.where(non_maximum_suppression(img,direction),img,0)
high = non_maxim>th_high
nei = neighbor(high)
low = np.where(nei,non_maxim>th_low,0)
return np.uint8(low)*255
def canny(img,th_low,th_high):
sobel_im,direction = sobel(img)
canny_img = hysteresis_thresholding(sobel_im, th_low, th_high, direction)
return canny_img
gaussian_value=[1,2,5]
thresholds = [[10,25],[30,75]]
fig = plt.figure(figsize=(13,13))
for i,sigma in enumerate(gaussian_value):
for j,ths in enumerate(thresholds):
plt.subplot(321+i*2+j)
gau_filter = make_gaussian(sigma)
gau = np.uint8(conv(img, gau_filter).squeeze())
canny_img = canny(gau,ths[1],ths[0])
plt.imshow(canny_img, cmap='gray')
plt.ylabel('$\sigma$={}'.format(sigma))
plt.xlabel('T_low={} T_high={}'.format(ths[1],ths[0]))
fig.tight_layout()
plt.show()

sigma 값이 커질수록 디테일이 작아지며 임계값이 높을 때 검출되는 에지의 숫자가 줄어든다.
OpenCV
opencv 같은 경우 가우시안과 케니를 다음과 같이 사용하면 된다.
직접 구현한 것과는 결과에서 차이가 발생한다.
cv_gau = cv2.GaussianBlur(img,(7,7),1)
plt.figure(figsize=(13,13))
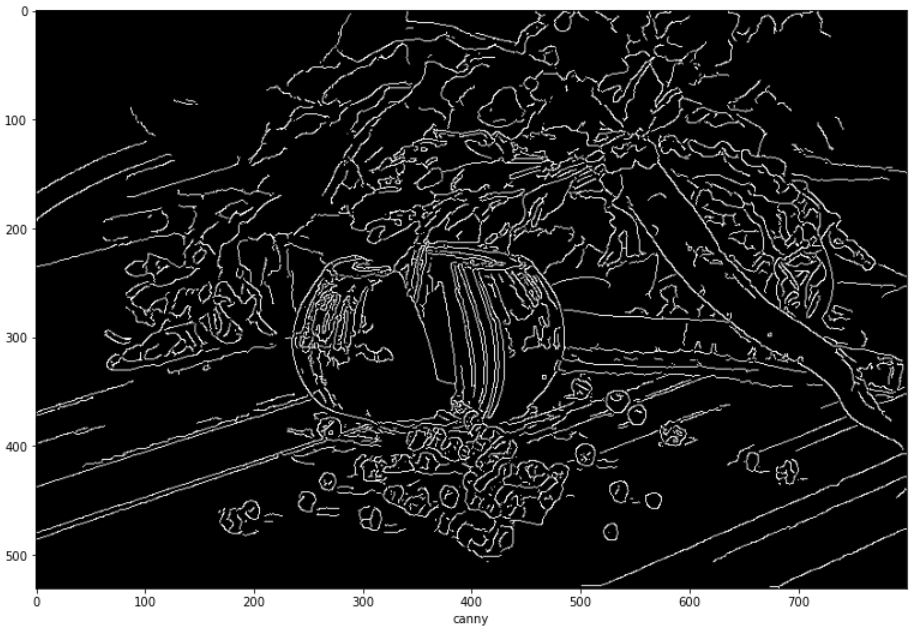
cv_canny = cv2.Canny(cv_gau,30,30*2.5)
plt.imshow(cv_canny,cmap='gray')
plt.xlabel("canny")
plt.show()
코드링크
1980년도 이전에는 주로 소벨 마스크가 에지 연산자로 사용되었다. 그런 상황에서 1980년에 Marr와 Hildreth가 발표한 논문은 에지 검출에 새로운 물줄기를 만들었다.
가우시안과 다중 스케일 효과
Marr와 Hildreth는 1차 미분 대신 2차 미분을 사용하는데, 미분을 적용하기 전에 가우시안으로 스무딩하는 전처리 과정을 중요하게 생각하였다.
가우시안 스무딩은 다음의 두 가지 효과를 제공한다.
- 잡음에 대처한다.
- 가우시안의 매개변수 \(\sigma\)를 조절해 다중 스케일(multi-scale) 효과를 얻는다.

\(sigma=0.5\)일 때 1차 미분과 2차 미분 결과를 보면 1차와 2차 미분 모두에서 영교차가 선명하게 나타난다.
반면 \(sigma\)가 커짐에 따라 폭이 작은 물체의 에지는 약해지는 것을 알 수 있다.
위의 사진을 통해 알 수 있는 것은 가우시안의 \(sigma\)를 조절해 스무딩 정도를 조절할 수 있으며 이는 에지 스케일을 정해준다는 것이다.
다음의 가우시안식을 보며 이산 공간에서 어떻게 구현할지 생각해보자
\[G(x)=\frac{1}{\sqrt{2 \pi} \sigma}e^{-\frac{x^{2}}{2 \sigma^{2}}}\]
import numpy as np
import matplotlib.pyplot as plt
import cv2
x = np.linspace(-20,20,100)
def gaussian(x,sigma):
return (1/(np.sqrt(2*np.pi)*sigma))*np.exp(-1*((x**2)/(2*(sigma**2))))
plt.plot(x,gaussian(x,0.5))
plt.plot(x,gaussian(x,1.0))
plt.plot(x,gaussian(x,2.0))
plt.plot(x,gaussian(x,5.0))
plt.ylim(0,1)
plt.legend(['$sigma$=0.5','$sigma$=1.0','$sigma$=2.0','$sigma$=5.0'])
plt.show()
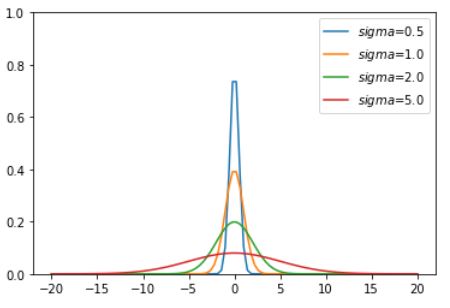
위 식에서 x가 0인 점에서 멀어지면 G(.)는 점점 작아지고, x의 크기가 크면 0에 아주 가까워진다. 따라서 샘플링할 때 적절한 크기의 마스크를 사용해야 한다. 만약 \(\sigma=2.0\)인 경우, 눈대중으로 짐작할 때 x는 절대값이 6일 때 0에 가까우므로 크기가 13정도인 마스크를 만들어 적용한다. 이것보다 작은 마스크는 오차가 커서 영상처리의 품질이 떨어지고, 크면 시간 효율만 나빠지고 크게 얻는 것이 없다.
LOG 필터
먼저 라플라시안(Laplacian)에 대해 설명한다.
\(\Delta^{2}f\)는 \(y\)와 \(x\)의 2차 편도함수 \(\frac{\partial^{2}f}{\partial y^{2}}\)와 \(\frac{\partial^{2}f}{\partial x^{2}}\)를 더한 것으로 다음과 같이 정의할 수 있다.
\[\Delta^{2}f(y,x)=\frac{\partial^{2}f}{\partial y^{2}}+\frac{\partial^{2}f}{\partial x^{2}}\]
이를 이산 공간에서 전개하면 다음과 같이 된다.
\[\Delta^{2}f(y,x)=\frac{\partial^2 f}{\partial y^{2}}+\frac{\partial^{2}f}{\partial x^{2}} \\
=(f(y+1,x)+f(y-1,x)-2f(y,x)) + (f(y,x+1)+f(y,x-1)-2f(y,x))\\
=f(y+1,x)+f(y-1,x)+f(y,x+1)+f(y,x-1)-4f(y,x) \\
이에 \ 해당하는 \ 필터 : \begin{pmatrix} 0&1&0 \\ 1&-4&1\\0&1&0 \end{pmatrix}\]
LOG 필터는 가우시안을 이산 필터로 근사화 한 후 라플라시안을 이산 필터로 근사화 하는 방식이다.
하지만 컨볼루션을 두 번 수행하기 때문에 계산 효율이 낮다.
이에 대한 대안으로 가우시안과 라플라시안의 연속 함수를 하나로 함치는 것이다.
입력 영상 f를 가우시안으로 컨볼루션한 후 라플라시안을 취하면 컨볼루션과 라플라시안 연산 간 결합법칙이 성립한다. 따라서 G에 라플라시안을 취한 후 그 결과를 f와 컨볼루션을 한 것과 같다.
이 식에서 가우시안에 라플라시안을 적용해 \(\Delta^{2}G\)를 LOG(Laplacian of Gaussian) 연산자 또는 LOG 필터라 부른다.
\[LOG(y,x) = \Delta^{2}(G(y,x)\circledast f(y,x))=(\Delta^{2}G(y,x)) \circledast f(y,x)\]
이 식을 좀 더 전개 해보자면 다음과 같다.
\[\Delta^{2}G(y,x)= \frac{\partial^2 G(y,x)}{\partial y^{2}}+\frac{\partial^2 G(y,x)}{\partial x^{2}}=\frac{\partial}{\partial y} \left( \frac{\partial G(y,x)}{\partial y} \right) + \frac{\partial}{\partial x} \left( \frac{\partial G(y,x)}{\partial x} \right) \\
=\frac{\partial}{\partial y} \left( -\left( \frac{y}{\sigma^{2}} \right) \frac{1}{2\pi \sigma^{2}} e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} \right) + \frac{\partial}{\partial x} \left( -\left( \frac{x}{\sigma^{2}} \right) \frac{1}{2\pi \sigma^{2}} e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} \right) \\
= \left( \frac{y^{2}}{\sigma^{4}}-\frac{1}{\sigma^2} \right) \frac{1}{2 \pi \sigma^{2}}e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} + \left( \frac{x^{2}}{\sigma^{4}}-\frac{1}{\sigma^2} \right) \frac{1}{2 \pi \sigma^{2}}e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} \\ = \left( \frac{y^{2}+x^{2}-2 \sigma^{2}}{\sigma^{4}} \right)G(y,x) \\
\therefore \Delta^{2}G(y,x)=\frac{y^{2}+x^{2}-2 \sigma^{2}}{\sigma^{4}}G(y,x)\]
def gaussian2d(x,y,sigma):
x2 = x**2
y2 = y**2
sigma2 = sigma**2
return (1/(2*np.pi*sigma2))*np.exp(-1*((x2+y2)/(2*sigma2)))
def LOG(sigma,plot=False):
size = int(sigma * 6)
if size %2 == 0:
size+=1
aran = np.arange(-1*(size//2),size//2+1)
XX, YY = np.meshgrid(aran,aran)
xx2 = XX**2
yy2 = YY**2
sigma2 = sigma**2
log = ((xx2+yy2-(2*sigma2))/(sigma2**2)) * gaussian2d(XX,YY,sigma)
if plot:
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_wireframe(XX, YY, log)
plt.show()
return log
LOG(5.0,True)
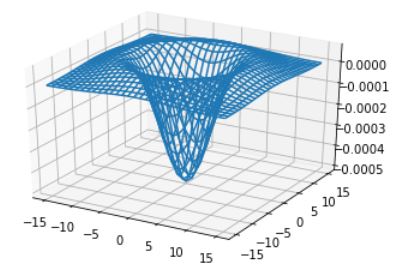
LOG 필터의 모양을 보면 방향과 무관한 등방성(isotropic) 성질을 가진다. 이는 사람의 시각과 비슷한 성질이다.
멕시코 모자(Mexican hat)라는 별명으로 불리기도 하고 밀짚모자라고 부르는 사람도 있는 것 같다.
이산 공간에서 근사화 할 때 필터의 크기는 6\(\sigma\)와 같거나 그것보다 큰 정수 중에 가장 작은 홀수를 필터의 크기로 취한다. 예를들어 \(\sigma=0.5\)일 때는 3x3 이다.
영교차 검출
이론적으로는 결과 영상을 \(g\)라고 했을 때, \(g(j,i)=0\)인 화소 중에서 마주보는 이웃이 서로 다른 부호를 가진 것을 영교차 점으로 보고 \(b(j,i)=1\)로 설정하면 된다. 하지만 연속 공간을 이산 공간으로 근사화했을 뿐 아니라 잡음의 영향이 있어 현실적인 규칙을 적용해야한다. 규칙은 다음과 같다.
- 여덟 개의 이웃 중에 마주보는 동-서, 남-북, 북동-남서, 북서-남동의 화소 쌍 네 개를 조사한다. 그들 중 두 개 이상이 서로 다른 부호를 가진다.
- 부호가 다른 쌍의 값 차이가 임계값을 넘는다.
구현하면 다음과 같다. conv 함수는 이전글에서 사용한 것과 동일하다.
def sign(a,b):
sign1 = np.logical_and(a<0,b>0)
sign2 = np.logical_and(b<0,a>0)
return np.logical_or(sign1,sign2)
def LOG_conv(img,filter,threshold=None):
log_img=conv(img,filter).squeeze()
if threshold == None:
threshold = np.max(log_img)*0.05
e_img = np.pad(log_img[:,1:],((0,0),(0,1)))
w_img = np.pad(log_img[:,:-1],((0,0),(1,0)))
n_img = np.pad(log_img[:-1,:],((1,0),(0,0)))
s_img = np.pad(log_img[1:, :], ((0,1), (0, 0)))
se_img = np.pad(s_img[:,1:],((0,0),(0,1)))
ne_img = np.pad(n_img[:, 1:], ((0, 0), (0, 1)))
sw_img = np.pad(s_img[:,:-1],((0,0),(1,0)))
nw_img = np.pad(n_img[:,:-1], ((0, 0), (1, 0)))
w_vs_e = np.int8(np.logical_and(np.absolute(w_img-e_img)>=threshold,sign(w_img,e_img)))
s_vs_n = np.int8(np.logical_and(np.absolute(n_img - s_img) >= threshold,sign(n_img,s_img)))
sw_vs_ne = np.int8(np.logical_and(np.absolute(sw_img - ne_img) >= threshold,sign(sw_img,ne_img)))
nw_vs_se = np.int8(np.logical_and(np.absolute(nw_img - se_img) >= threshold,sign(nw_img,se_img)))
return np.uint8(w_vs_e+s_vs_n+sw_vs_ne+nw_vs_se>=1)*255
\(\sigma\) 값을 다르게 하면 다음과 같다. 임계값은 영상 g의 최대값에 0.05를 곱했다.
img = cv2.imread('./data/food.jpg',cv2.IMREAD_GRAYSCALE)
sigma_value = [1.0,2.0,4.0,8.0]
fig = plt.figure(figsize=(13,13))
for i in range(1,5):
plt.subplot(220+i)
log_filter = LOG(sigma_value[i-1])
log_img = LOG_conv(img,log_filter)
plt.imshow(log_img,cmap='gray')
plt.xlabel('$sigma$={}'.format(sigma_value[i-1]))
fig.tight_layout()
plt.show()

결과를 보면 \(\sigma\)가 작을 때에는 세밀한 에지까지 검출되는 반면, 커지면 세밀한 부분은 점점 사라지고 큰 규모의 에지만 남는다.
31 May 2020
•
TIL
컴퓨터비전책 꾸준히 구현중인데 책 내용이 좋은거 같다.
중간중간 막힐 때가 있기는 하지만 아직까지 엄청 큰 무리가 나진않는다.
솔직히 수식 마크다운으로 옮기고 나중에 내가 볼때 어떻게 해야 이해가 갈까 그 생각 때문에 오래걸리는 것 같다.
핸즈온 머신러닝도 빨리 읽고 싶은데 통계부터 공부하는게 맞는거 같다 ㅜㅜ
TID
- 2020/05/29
-
이미지 피라미드 공부 및 구현
-
2020/05/30
- 이상엽 math5강
- 베이즈 이론 간단 정리
- 모폴로지 공부 및 구현
-
2020/05/31
- 이상엽 math6강
- 엣지 검출의 기초 공부 및 구현
- 이항분포 간단 정리
31 May 2020
•
Statistics
이항 분포
이항분포는 ‘확률 p로 앞이 나오는 동전을 n번 던졌을 때 앞이 몇 번 나올지’의 분포이다. 즉 확률 p로 1, 확률 q=(1-p)로 0이 나오는 독립적인 확률 변수 \(Z_{1},...,Z_{n}\)을 두면, \(X \equiv Z_{1}+...+Z_{n}\)의 분포가 이항분포가 된다.
이항 분포는 n과 p에 따라 분포의 모양이 바뀌어서 \(Bn(n,p)\)처럼 나타낸다.
균등분포(생길 수 있는 값으로 n개의 경우가 있을 때 확률이 모두 1/n인 분포)인 동전을 던져 n=7번 던져 앞면이 세 번 나오는 확률 P(X=3)을 찾아보자.
- 뒤뒤뒤뒤앞앞앞 = \(p^{3}q^{4}\)
- 뒤뒤뒤앞앞앞뒤 = \(p^{3}q^{4}\)
- …
이렇게 총 35개의 \(p^{3}q^{4}\)가 나오는데 이를 이용해 일반화를 하면 다음과 같다.
\[P(X=k)=_{n}\mathrm{C}_{k}p^{k}q^{n-k} \qquad (k=0,1,2,...,n)\]
순열과 조합
순열(Permutation)
n명의 사람 중에서 k명의 사람을 뽑아 한 줄로 나란히 늘어놓는 방법을 세는 방식. 첫 번째가 n가지 다음은 n-1 이런식으로 간다면 순열은 다음과 같이 표현된다.
\[_{n}\mathrm{P}_{k}=n(n-1)(n-2)...(n-k+1)\]
팩토리얼을 사용해 다음과 같이 쓰는 경우가 많다.
\[_{n}\mathrm{P}_{k}=\frac{n!}{(n-k)!}\]
조합(Combination)
조합은 n명의 사람 중에서 k 명의 사람을 고르지만 순서에 상관 없이 고르는 방식이다. 즉 1,2,3을 선택한 것과 3,2,1을 선택한 것은 동일하다.
\(_{n}\mathrm{C}_{k}\)로 표기하고 이항계수라고 불리기도 한다 순서를 생각하면 \(_{n}\mathrm{P}_{k}\)가지지만, 선택한 k명의 사람을 나열(\(_{k}\mathrm{P}_{k}=k!가지\))하는 방법의 차이는 무시하므로, \(_{n}\mathrm{P}_{k}\)를 k!로 나누어야 한다.
\[_{n}\mathrm{C}_{k}=\frac{_{n}\mathrm{P}_{k}}{k!}=\frac{n!}{k!(n-k)!}\]
이항분포의 확률 계산에 나오는 경우의 수가 \(_{n}\mathrm{C}_{k}\)와 일치하는 이유는 패턴 가짓수는 길이가 n인 열에서 앞이 되는 곳을 k개 지정하는 조합의 수와 같기 때문이다.
코드링크
에지(Edge)
에지란 영상의 명암, 컬러, 또는 텍스처와 같은 특성이 급격히 변하는 지점이다. 모든 에지 검출 알고리즘은 변화를 측정하고 변화량이 큰 곳을 에지로 취하는 원리를 따른다.
변화량을 구하기 위해 보통 도함수(derivative)를 사용하는데, 컴퓨터 비전에서는 연속 공간이 아닌 이산 공간에서 정의된다. 따라서 이산 공간에서 도함수를 근사화하는 방법을 고안해야 한다.
\[f'(x)=\frac{df}{dx} = \frac{f(x+\Delta x)-f(x)}{\Delta x}=f(x+1)-f(x) \\
\therefore mask= (-1,1)\]
위와 같이 이에 해당하는 마스크는 (-1,1)이다. 마스크 연산이후 절대값이 임계값을 넘는 값을 에지 화소(edge pixel)라고 하고 이러한 마스크는 에지 마스크 또는 에지 연산자(edge operator)라고 한다.
에지 모델과 연산자
다음 그림은 계단 에지(step edge)와 램프 에지(ramp edge)라 불리는 두 종류의 에지를 가진 영상이다.
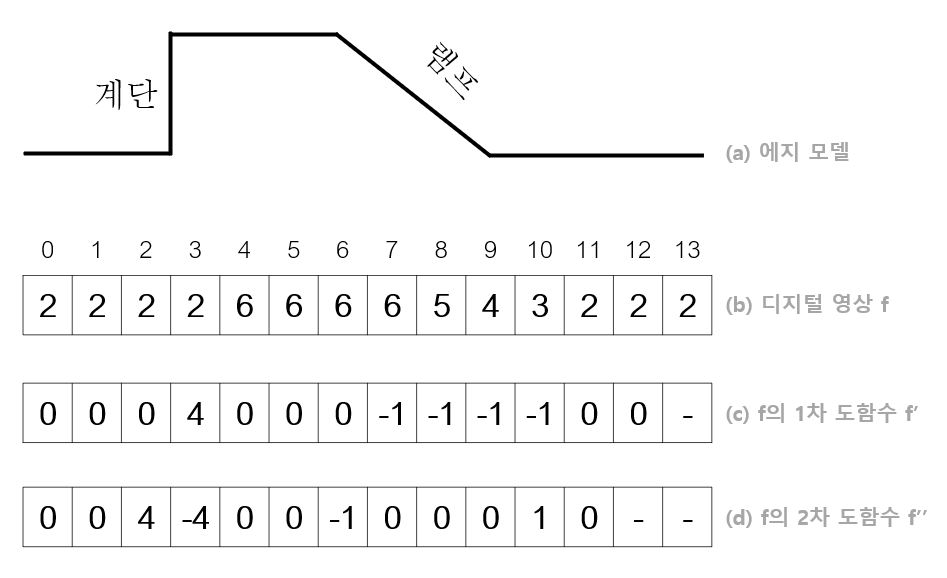
그림의 c는 영상 f를 한 번 미분한 1차 도함수이고, d는 1차 도함수를 한 번 더 미분한 2차 도함수이다. 1차 미분을 살펴보면 계단 에지에서 봉우리(peak)가 나타난다. 봉우리의 두께가 1이므로 계단 에지만 존재하는 경우 에지를 찾는 일이 매우 간단하다.
하지만 실제 데이터에서는 카메라로 영상을 획득할 때 완벽하게 초점을 맞추기 불가능하기 때문에 주로 램프 에지가 나타난다. 위 그림에서 7부터 10에 걸쳐 램프 에지가 나타나 두께가 4이다. 에지의 정확한 위치를 찾는 일을 위치 찾기(Localization)이라 한다.
램프에지와 계단 에지 둘 모두에서 1차 미분 결과로 봉우리가 나타나고 2차 미분 결과에서 영교차(zero crossing)이 나타난 것을 볼 수 있다. 이렇게 봉우리와 영교차를 찾는것이 에지 검출의 기본원리이다.
에지 검출에서 고려해야 할 문제중 불완전한 광학 때문에 발생하는 잡음이 있다. 예를들어 실제로는 같은 명암이지만 이미지상에서 여러가지 요인으로 값이 조금씩 차이나는 문제이다. 그래서 에지 연산자를 적용하기 전, 잡음을 제거하기 위해 스무딩 연산을 적용하기도 한다.
아래의 그림은 에지 검출에서 쓰는 여러가지 마스크이다.
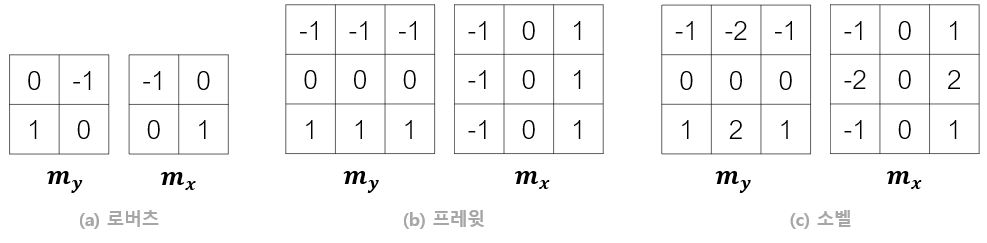
이중 소벨 연산자(Sobel operator)와 프레윗 연산자(Prewitt operator)는 해당 픽셀의 아래와 윗 행까지 같이 고려한다. 즉, 스무딩 효과가 내포되어 있다. 소벨 연산자는 가까운 화소에 더 큰 가중치를 준다는 차이가 있다. 로버츠 연산자(Roberts operator)는 대칭이 아닐 뿐만 아니라 너무 작아 잘 사용하지 않고 소벨이 가장 널리 사용된다.
에지 강도와 에지 방향
그레디언트는 벡터이므로 에지 강도(edge magnitude(혹은 edge strength))와 에지 방향(edge direction)을 구할 수 있다. 다음 식은 그레디언트에서 에지 강도와 그레이언트 방향을 계산하는 식이다.
\[그레디언트 : \Delta f =\begin{pmatrix} \frac{\partial f}{\partial y},\frac{\partial f}{\partial x} \end{pmatrix}=(d_{x},d_{y}) \\
에지 \ 강도 : S(y,x)=magnitude(\Delta f) = \sqrt{d_{y}^{2}+d_{x}^{2}} \\
그레디언트 \ 방향 : D(y,x) = arctan(\frac{d_y}{d_x})\]
에지 강도는 화소 (y,x)가 에지일 가능성 또는 신뢰도(confidence)를 나타내는 값이다.
코드구현
이번 구현은 그레이 스케일이미지에서 할 것이다.
import numpy as np
import cv2
import matplotlib.pyplot as plt
img =cv2.cvtColor(cv2.imread('./data/food.jpg'),cv2.COLOR_BGR2GRAY)
plt.imshow(img,cmap='gray')
plt.show()

컨볼루션 연산은 이전에 구현한 im2col을 사용하자 이전글링크
이전과의 차이점은 gray scale 때의 처리를 추가하였고 return에서 int로 캐스팅 하지 않는다.
def im2col(input_data, filter_h, filter_w):
H, W, C = input_data.shape
u_pad_h = (filter_h-1)//2
d_pad_h = (filter_h-1)//2
l_pad_w = (filter_w-1)//2
r_pad_w = (filter_w-1)//2
if (filter_h-1) %2 ==1:
u_pad_h +=1
if (filter_w-1)%2 ==1:
l_pad_w +=1
input_data = cv2.copyMakeBorder(input_data, u_pad_h, d_pad_h, l_pad_w, r_pad_w, cv2.BORDER_REPLICATE)
if C==1:
input_data= np.expand_dims(input_data,-1)
img = np.transpose(input_data,(2,0,1))
col = np.zeros(( C, filter_h, filter_w, H, W))
for y in range(filter_h):
y_max = y + H
for x in range(filter_w):
x_max = x + W
col[:, y, x, :, :] = img[:, y:y_max:1, x:x_max:1]
col = np.transpose(col,(0,3,4,1,2)).reshape(C*H*W, -1)
return col
def conv(img,filter):
filter_h ,filter_w = filter.shape
if len(img.shape) ==3:
img_h,img_w,c = img.shape
elif len(img.shape)==2:
img_h,img_w = img.shape
c=1
img = np.expand_dims(img,-1)
else:
print("Length of image shape must over 2")
return
col = im2col(img,filter_h,filter_w)
col_filetr = filter.reshape((1,-1)).T
out = np.dot(col, col_filetr)
return np.transpose(out.reshape((c, img_h, img_w)),(1, 2,0))
이번 구현에서는 소벨 마스크만 사용해보기로 한다. 만약 다른 커널이 필요하면 다음과 같은 방식으로 커스텀하면 된다.
원래 외곽의 값들은 0이기 때문에 이에대한 처리를 해주자
sobel_mask_y = np.array([[-1,-2,-1],
[0,0,0],
[1,2,1]])
sobel_mask_x = np.array([[-1,0,1],
[-2,0,2],
[-1,0,1]])
dy_image =conv(img,sobel_mask_y).squeeze()
dx_image =conv(img,sobel_mask_x).squeeze()
dy_image[0,:] = dy_image[-1,:] = 0 # 맨 끝부분은 0으로 처리한다.
dx_image[:,0] = dx_image[:,-1] = 0
S = np.uint8(np.sqrt((dy_image**2)+(dx_image**2)))
# image plot
fig = plt.figure(figsize=(13,13))
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.subplot(222)
plt.imshow(S,cmap='gray')
plt.xlabel('Edge strength')
plt.subplot(223)
plt.imshow(np.uint8(abs(dx_image)),cmap='gray') # 변화량은 음수값도 나오기 때문에 절대값 연산을 해야한다.
plt.xlabel('dx')
plt.subplot(224)
plt.imshow(np.uint8(abs(dy_image)),cmap='gray')
plt.xlabel('dy')
fig.tight_layout()
plt.show()

OpenCV
opencv에서는 소벨연산을 하는 함수자체가 따로 제공된다. 소벨 연산이 필요한 경우 cv2.Sobel 함수를 사용하면 된다.
cv_sobel_y = cv2.Sobel(img,cv2.CV_64F,0,1)
cv_sobel_x = cv2.Sobel(img,cv2.CV_64F,1,0)
cv_s = np.uint8(np.sqrt((cv_sobel_x**2)+(cv_sobel_y**2)))
fig = plt.figure(figsize=(13,13))
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.subplot(222)
plt.imshow(cv_s,cmap='gray')
plt.xlabel('Edge strength')
plt.subplot(223)
plt.imshow(np.uint8(abs(cv_sobel_x)),cmap='gray')
plt.xlabel('dx')
plt.subplot(224)
plt.imshow(np.uint8(abs(cv_sobel_y)),cmap='gray')
plt.xlabel('dy')
fig.tight_layout()
plt.show()












