1980년도 이전에는 주로 소벨 마스크가 에지 연산자로 사용되었다. 그런 상황에서 1980년에 Marr와 Hildreth가 발표한 논문은 에지 검출에 새로운 물줄기를 만들었다.
가우시안과 다중 스케일 효과
Marr와 Hildreth는 1차 미분 대신 2차 미분을 사용하는데, 미분을 적용하기 전에 가우시안으로 스무딩하는 전처리 과정을 중요하게 생각하였다.
가우시안 스무딩은 다음의 두 가지 효과를 제공한다.
- 잡음에 대처한다.
- 가우시안의 매개변수 \(\sigma\)를 조절해 다중 스케일(multi-scale) 효과를 얻는다.

\(sigma=0.5\)일 때 1차 미분과 2차 미분 결과를 보면 1차와 2차 미분 모두에서 영교차가 선명하게 나타난다.
반면 \(sigma\)가 커짐에 따라 폭이 작은 물체의 에지는 약해지는 것을 알 수 있다.
위의 사진을 통해 알 수 있는 것은 가우시안의 \(sigma\)를 조절해 스무딩 정도를 조절할 수 있으며 이는 에지 스케일을 정해준다는 것이다.
다음의 가우시안식을 보며 이산 공간에서 어떻게 구현할지 생각해보자
\[G(x)=\frac{1}{\sqrt{2 \pi} \sigma}e^{-\frac{x^{2}}{2 \sigma^{2}}}\]import numpy as np
import matplotlib.pyplot as plt
import cv2
x = np.linspace(-20,20,100)
def gaussian(x,sigma):
return (1/(np.sqrt(2*np.pi)*sigma))*np.exp(-1*((x**2)/(2*(sigma**2))))
plt.plot(x,gaussian(x,0.5))
plt.plot(x,gaussian(x,1.0))
plt.plot(x,gaussian(x,2.0))
plt.plot(x,gaussian(x,5.0))
plt.ylim(0,1)
plt.legend(['$sigma$=0.5','$sigma$=1.0','$sigma$=2.0','$sigma$=5.0'])
plt.show()
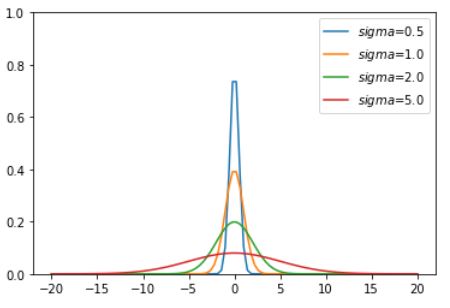
위 식에서 x가 0인 점에서 멀어지면 G(.)는 점점 작아지고, x의 크기가 크면 0에 아주 가까워진다. 따라서 샘플링할 때 적절한 크기의 마스크를 사용해야 한다. 만약 \(\sigma=2.0\)인 경우, 눈대중으로 짐작할 때 x는 절대값이 6일 때 0에 가까우므로 크기가 13정도인 마스크를 만들어 적용한다. 이것보다 작은 마스크는 오차가 커서 영상처리의 품질이 떨어지고, 크면 시간 효율만 나빠지고 크게 얻는 것이 없다.
LOG 필터
먼저 라플라시안(Laplacian)에 대해 설명한다.
\(\Delta^{2}f\)는 \(y\)와 \(x\)의 2차 편도함수 \(\frac{\partial^{2}f}{\partial y^{2}}\)와 \(\frac{\partial^{2}f}{\partial x^{2}}\)를 더한 것으로 다음과 같이 정의할 수 있다.
이를 이산 공간에서 전개하면 다음과 같이 된다.
\[\Delta^{2}f(y,x)=\frac{\partial^2 f}{\partial y^{2}}+\frac{\partial^{2}f}{\partial x^{2}} \\ =(f(y+1,x)+f(y-1,x)-2f(y,x)) + (f(y,x+1)+f(y,x-1)-2f(y,x))\\ =f(y+1,x)+f(y-1,x)+f(y,x+1)+f(y,x-1)-4f(y,x) \\ 이에 \ 해당하는 \ 필터 : \begin{pmatrix} 0&1&0 \\ 1&-4&1\\0&1&0 \end{pmatrix}\]LOG 필터는 가우시안을 이산 필터로 근사화 한 후 라플라시안을 이산 필터로 근사화 하는 방식이다.
하지만 컨볼루션을 두 번 수행하기 때문에 계산 효율이 낮다.
이에 대한 대안으로 가우시안과 라플라시안의 연속 함수를 하나로 함치는 것이다.
입력 영상 f를 가우시안으로 컨볼루션한 후 라플라시안을 취하면 컨볼루션과 라플라시안 연산 간 결합법칙이 성립한다. 따라서 G에 라플라시안을 취한 후 그 결과를 f와 컨볼루션을 한 것과 같다.
이 식에서 가우시안에 라플라시안을 적용해 \(\Delta^{2}G\)를 LOG(Laplacian of Gaussian) 연산자 또는 LOG 필터라 부른다.
이 식을 좀 더 전개 해보자면 다음과 같다.
\[\Delta^{2}G(y,x)= \frac{\partial^2 G(y,x)}{\partial y^{2}}+\frac{\partial^2 G(y,x)}{\partial x^{2}}=\frac{\partial}{\partial y} \left( \frac{\partial G(y,x)}{\partial y} \right) + \frac{\partial}{\partial x} \left( \frac{\partial G(y,x)}{\partial x} \right) \\ =\frac{\partial}{\partial y} \left( -\left( \frac{y}{\sigma^{2}} \right) \frac{1}{2\pi \sigma^{2}} e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} \right) + \frac{\partial}{\partial x} \left( -\left( \frac{x}{\sigma^{2}} \right) \frac{1}{2\pi \sigma^{2}} e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} \right) \\ = \left( \frac{y^{2}}{\sigma^{4}}-\frac{1}{\sigma^2} \right) \frac{1}{2 \pi \sigma^{2}}e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} + \left( \frac{x^{2}}{\sigma^{4}}-\frac{1}{\sigma^2} \right) \frac{1}{2 \pi \sigma^{2}}e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}} \\ = \left( \frac{y^{2}+x^{2}-2 \sigma^{2}}{\sigma^{4}} \right)G(y,x) \\ \therefore \Delta^{2}G(y,x)=\frac{y^{2}+x^{2}-2 \sigma^{2}}{\sigma^{4}}G(y,x)\]def gaussian2d(x,y,sigma):
x2 = x**2
y2 = y**2
sigma2 = sigma**2
return (1/(2*np.pi*sigma2))*np.exp(-1*((x2+y2)/(2*sigma2)))
def LOG(sigma,plot=False):
size = int(sigma * 6)
if size %2 == 0:
size+=1
aran = np.arange(-1*(size//2),size//2+1)
XX, YY = np.meshgrid(aran,aran)
xx2 = XX**2
yy2 = YY**2
sigma2 = sigma**2
log = ((xx2+yy2-(2*sigma2))/(sigma2**2)) * gaussian2d(XX,YY,sigma)
if plot:
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_wireframe(XX, YY, log)
plt.show()
return log
LOG(5.0,True)
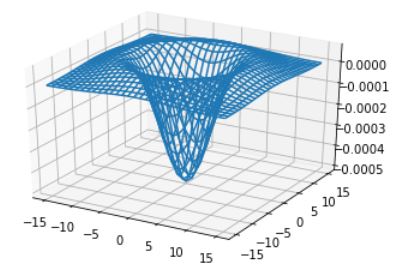
LOG 필터의 모양을 보면 방향과 무관한 등방성(isotropic) 성질을 가진다. 이는 사람의 시각과 비슷한 성질이다.
멕시코 모자(Mexican hat)라는 별명으로 불리기도 하고 밀짚모자라고 부르는 사람도 있는 것 같다.
이산 공간에서 근사화 할 때 필터의 크기는 6\(\sigma\)와 같거나 그것보다 큰 정수 중에 가장 작은 홀수를 필터의 크기로 취한다. 예를들어 \(\sigma=0.5\)일 때는 3x3 이다.
영교차 검출
이론적으로는 결과 영상을 \(g\)라고 했을 때, \(g(j,i)=0\)인 화소 중에서 마주보는 이웃이 서로 다른 부호를 가진 것을 영교차 점으로 보고 \(b(j,i)=1\)로 설정하면 된다. 하지만 연속 공간을 이산 공간으로 근사화했을 뿐 아니라 잡음의 영향이 있어 현실적인 규칙을 적용해야한다. 규칙은 다음과 같다.
- 여덟 개의 이웃 중에 마주보는 동-서, 남-북, 북동-남서, 북서-남동의 화소 쌍 네 개를 조사한다. 그들 중 두 개 이상이 서로 다른 부호를 가진다.
- 부호가 다른 쌍의 값 차이가 임계값을 넘는다.
구현하면 다음과 같다. conv 함수는 이전글에서 사용한 것과 동일하다.
def sign(a,b):
sign1 = np.logical_and(a<0,b>0)
sign2 = np.logical_and(b<0,a>0)
return np.logical_or(sign1,sign2)
def LOG_conv(img,filter,threshold=None):
log_img=conv(img,filter).squeeze()
if threshold == None:
threshold = np.max(log_img)*0.05
e_img = np.pad(log_img[:,1:],((0,0),(0,1)))
w_img = np.pad(log_img[:,:-1],((0,0),(1,0)))
n_img = np.pad(log_img[:-1,:],((1,0),(0,0)))
s_img = np.pad(log_img[1:, :], ((0,1), (0, 0)))
se_img = np.pad(s_img[:,1:],((0,0),(0,1)))
ne_img = np.pad(n_img[:, 1:], ((0, 0), (0, 1)))
sw_img = np.pad(s_img[:,:-1],((0,0),(1,0)))
nw_img = np.pad(n_img[:,:-1], ((0, 0), (1, 0)))
w_vs_e = np.int8(np.logical_and(np.absolute(w_img-e_img)>=threshold,sign(w_img,e_img)))
s_vs_n = np.int8(np.logical_and(np.absolute(n_img - s_img) >= threshold,sign(n_img,s_img)))
sw_vs_ne = np.int8(np.logical_and(np.absolute(sw_img - ne_img) >= threshold,sign(sw_img,ne_img)))
nw_vs_se = np.int8(np.logical_and(np.absolute(nw_img - se_img) >= threshold,sign(nw_img,se_img)))
return np.uint8(w_vs_e+s_vs_n+sw_vs_ne+nw_vs_se>=1)*255
\(\sigma\) 값을 다르게 하면 다음과 같다. 임계값은 영상 g의 최대값에 0.05를 곱했다.
img = cv2.imread('./data/food.jpg',cv2.IMREAD_GRAYSCALE)
sigma_value = [1.0,2.0,4.0,8.0]
fig = plt.figure(figsize=(13,13))
for i in range(1,5):
plt.subplot(220+i)
log_filter = LOG(sigma_value[i-1])
log_img = LOG_conv(img,log_filter)
plt.imshow(log_img,cmap='gray')
plt.xlabel('$sigma$={}'.format(sigma_value[i-1]))
fig.tight_layout()
plt.show()

결과를 보면 \(\sigma\)가 작을 때에는 세밀한 에지까지 검출되는 반면, 커지면 세밀한 부분은 점점 사라지고 큰 규모의 에지만 남는다.
Comments