30 May 2020
•
Statistics
베이즈 정리
조건부 확률의 응용이며 일종의 역문제를 생각한다. 역문제는 간단히 말해 결과에서 원인을 찾는 문제이다.
원인 \(X\)를 직접적으로 관측, 측정할 수 없을 때 거기서 일어난 결과 \(Y\)를 보고 원인 \(X\)를 추측하는 것이다.
여기서 \(P(원인)\)을 사전확률, \(P(원인 \mid 결과)\)를 사후확률이라고 한다. 베이즈 공식은 사후확률을 구하는 것이다.
ex1)
Q. 어떤 게임에서 몬스터를 쓰러뜨리면 보물 상자를 얻을 수 있다. 보물 상자는 확률 2/3로 함정이다. 함정의 낌새는 스킬로 판정가능하나, 스킬레벨이 낮아 확률 1/4로 판정이 잘못된다.
몬스터를 쓰러뜨리고 보물 상자에 스킬을 썼는데 ‘함정의 낌새가 없다’는 판정이 나왔을 때 실제로 보물 상자가 함정일 확률’은 얼마인가?
\(P(X=함정있음) = \frac{2}{3} \\
P(Y=낌새없음,X=함정있음) = \frac{1}{4} \times \frac{2}{3} = \frac{1}{6} \\
P(Y=낌새있음,X=함정없음) = \frac{3}{4} \times \frac{1}{3} = \frac{1}{4} \\
P(Y=낌새없음) = P(Y=낌새없음,X=함정있음)+P(Y=낌새있음,X=함정없음)=\frac{1}{6} + \frac{1}{4}=\frac{5}{12} \\
P(X=함정있음|Y=낌새없음)=\frac{P(X=함정있음,Y=낌새없음)}{P(Y=낌새없음)}\\ = \frac{P(Y=낌새없음,X=함정있음)}{P(Y=낌새없음)}=\frac{\frac{1}{4}}{\frac{5}{12}}=\frac{3}{5}\)
ex2)
Q. 방패를 골랐을 때 1/2 확률로 보통, 1/3 확률로 상급, 1/6로 특제이다. 방패별 성능은 다음과 같다.
- 보통 방패는 1/18 확률로 몬스터의 공격을 피한다.
- 상급 방패는 1/6 확률로 몬스터의 공격을 피한다.
- 특제 방패는 1/3 확률로 몬스터의 공격을 피한다.
1.주운 방패를 장비했을 때 몬스터의 공격을 피할 확률은?
\[P(Y=피함)=P(Y=피함,X=보통)+P(Y=피함,X=상급)+{P(Y=피함,X=특제)}\\
=\frac{1}{18} \times \frac{1}{2}+\frac{1}{6} \times \frac{1}{3}+\frac{1}{3} \times \frac{1}{6}=\frac{5}{36}\]
2.주운 방패를 장비하고 몬스터의 공격을 받았는데 공격을 피했다. 이때 방패가 특제일 확률은?
\[P(X=특제|Y=피함)=\frac{P(X=특제,Y=피함)}{P(Y=피함)}=\frac{\frac{1}{18}}{\frac{5}{36}}=\frac{2}{5}\]
위의 예제들로 부터 결과로부터 원인을 구하는 방법을 공식화 할 수 있다. X를 원인, Y를 결과라고 했을 때 다음이 성립한다.
\[P(X=목표원인|Y=결과)=\frac{P(X=목표원인,Y=결과)}{\sum_{원인}P(X=원인,Y=결과)}\]
코드링크
모폴로지 (Morphology)
모폴로지는 원래 생물학자들이 동물이나 식물이 보여주는 모양을 지칭하기 위해 사용하는 용어이다.
컴퓨터 비전에서는 생물과 구분하기 위해 수학적 모폴로지(mathermatical morphology)라는 용어를 사용하기도 한다.
물론 간단하게 모폴로지, 영상 모폴로지라고 부르는 경우가 더 많다.
모폴로지는 이진 영상에서 작동하는 이진 모폴로지, 명암 영상에서 작동하는 명암 모폴로지로 나뉜다.
이진 모폴로지
모폴로지는 구조요소(Structurgin element)를 사용해 이진 영상에 있는 연결요소의 모양을 조작한다.
다음의 그림은 몇 가지 대표적인 구조요소이다.
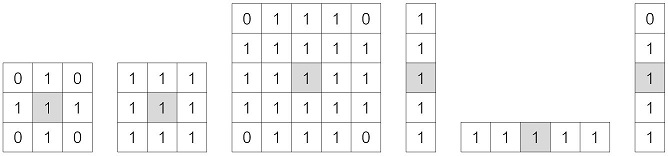
모폴로지에서 구조요소는 집합으로 표현하는데, 값이 1인 요소만 집합에 속한다. 최우측에 있는 구조요소처럼 비대칭일수도있다.
집합 \(S\)를 \(t=(t_y,t_x)\) 만큼 이동시켜 얻은 새로운 집합을 S_t라고 표기하고 다음과 같은 식으로 정의한다.
\[S_{t}= \left\{ s + t | s \in S \right\}\]
가장 기본적인 두 가지 모폴로지 연산은 팽창(dilation)과 침식(erosion)이다.
팽창은 \(f\)의 1인 화소에 구조요소 \(S\)를 씌우고 \(S\)의 1인 점과 겹치는 곳을 모두 1로 바꾼다(합집합).
결과적으로 영상에 있는 연결요소는 구조요소만큼 외부로 팽창한다.
반대로 침식은 \(f\)의 어떤 화소에 구조요소를 씌웠을 때, 구조요소의 1인 곳과 겹치는 곳이 모두 1인 경우만 그 화소를 1로 결정한다(교집합).
식으로 표현하면 다음과 같다.
\[팽창 : f \oplus S = \underset{x \in f}{\cup} S_{x} \\
침식 : f \circleddash S = \left\{ x | x+s \in f, \forall s \in S \right\}\]
여기서 f는 1을 갖는 화소의 집합이다. x in f는 영상 f에서 1을 갖는 화소 x를 의미한 다. s와 x는 좌표이다.
팽창과 침식 연산을 이용해 열기(opening)과 닫기(closing) 연산을 다음과 같이 정의한다.
\[열기 : f \circ S = (f \circleddash S)\oplus S \\
닫기 : f \cdot S = (f \oplus S)\circleddash S\]
열기는 침식이후 팽창, 닫기는 팽창이후 침식이다.
ex)

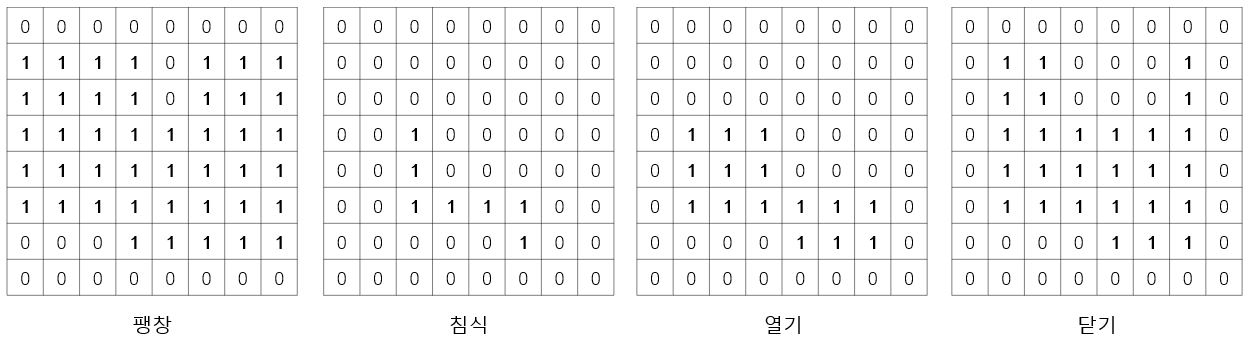
\(x=(1,1)\) 일 때, \(s_{x} 혹은 x+s의 집합=\left\{ (0,-1),(1,1),(1,2) \right\}\) 이다. \(s_{x}\)의 합집합은 1이기 때문에 팽창연산에서는 1, \(x+s\)의 모든 요소가 \(f\)에서 1을 갖는 요소가 아니므로 0이 된다.
팽창연산은 이와같이 홈을 메우는데 사용되는 것을 알 수 있다. 홈을 메우되 원래 크기를 유지하고 싶을 때 침식을 추가로 적용한 닫기 연산을 하면 된다.
침식은 구조요소보다 작은 크기의 돌출 부분을 깎는다. 마찬가지로 침식된 영상에서 원래 크기로 복원하기 위해 팽창을 추가한 열기 연산을 한다.
명암 모폴로지
이진 모폴로지는 평면 모양의 패인 곳을 메우거나 튀어나온 곳을 깎는 역할을 한다면, 명암 모폴로지는 명암을 지표면부터의 높이로 간주하여 이 지형의 골짜기를 메우거나 봉우리를 깎는 효과를 제공한다.
\[명암 팽창(평편하지 않은 구조요소) : (f \oplus S)(i,j) = \underset{(y,x) \in S}{max}(f(j-y,i-x) + S(y,x)) \\
명암 침식(평편하지 않은 구조요소) : (f \circleddash S)(i,j) = \underset{(y,x) \in S}{max}(f(j+y,i+x) - S(y,x))\]
팽창은 지형을 솟구치게 하기 위해, 영상에 구조요소 값을 더해준 후 최대값을 취한다. 이때 구조요소의 좌표\((y,x)\)를 빼주는데 구조요소를 180도 회전해 적용하는 셈이다.
예를들어 구조요소가 {(0,-1),(0,0),(0,1),(0,2)}인 오른쪽으로 팽창을 해야하는데 덧셋을 하게 되면 오른쪽 값을 참조해서 오른쪽으로 팽창을 하지 못한다.
따라서 왼쪽의 값을 참조하기 위해 뺄셈을 한다.
영상의 경계에서 구조요소를 씌우면 구조요소의 일부가 영상 밖으로 걸치게 되는데, 이런 경우를 처리하기 위해 팽창에서는 -무한대, 침식에서는 +무한대로 대체한다.
실제 응용에서는 적합한 구조요소를 설계하는 일 자체가 번거롭기 때문에 보통 S를 제거해 다음과 같은 식을 사용한다.
\[명암 팽창(평편하지 않은 구조요소) : (f \oplus S)(i,j) = \underset{(y,x) \in S}{max}f(j-y,i-x) \\
명암 침식(평편하지 않은 구조요소) : (f \circleddash S)(i,j) = \underset{(y,x) \in S}{max}f(j+y,i+x)\]
이진 모폴로지와 마찬가지로 팽찬은 영상을 더 밝게 만들거나 밝은 영역을 넓혀주며, 침식은 영상을 더 어둡게 만들거나 어두운 영역을 넓혀준다.
모폴로지 연산은 공장에서 생산되는 기계 부품, 반도체 칩, LED 소자의 결함 탐지와 같은 응용 문제를 해결하는데 사용되기도 한다.
코드 구현
우선 영상을 이진화 한다.
import numpy as np
import cv2
import matplotlib.pyplot as plt
img =cv2.cvtColor(cv2.imread('./data/baboon.jpg'),cv2.COLOR_BGR2RGB)
_,binary_im = cv2.threshold(cv2.cvtColor(img,cv2.COLOR_BGR2GRAY),175,255,cv2.THRESH_BINARY)
fig =plt.figure()
plt.subplot(121)
plt.imshow(img)
plt.subplot(122)
plt.imshow(binary_im,cmap='gray')
fig.tight_layout()
plt.show()
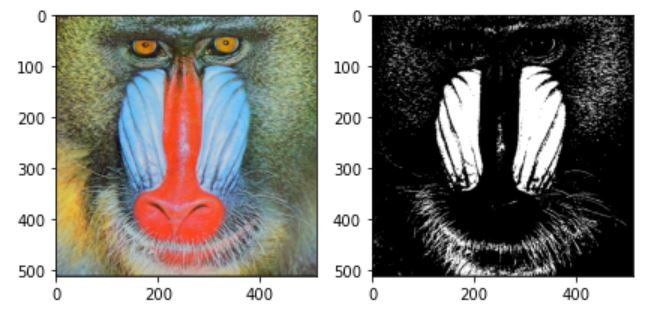
이진화에서는 convolution 연산보다 1이 나타난 index를 한꺼번에 더해주는 게 더 빠르기 때문에 다음과 같이 구현했다. 침식과 팽창은 범위를 반대로 했다.
def bi_dilation(img,kernel,ker_center=None):
ker_H, ker_W = kernel.shape
if ker_center == None:
ker_center = np.array([ker_H//2,ker_W//2])
out = np.zeros_like(img)
img//=np.max(img)
for y in range(ker_H):
for x in range(ker_W):
if kernel[y,x]:
y_diff = y-ker_center[0]
x_diff = x-ker_center[1]
h_pad = abs(y_diff)
w_pad = abs(x_diff)
if y_diff >0 and x_diff >0:
out+=np.pad(img[:-1*y_diff,:-1*x_diff],((h_pad,0),(w_pad,0)),'constant',constant_values=0)
elif y_diff >0:
out += np.pad(img[:-1*y_diff,-1*x_diff:], ((h_pad,0), (0, w_pad)), 'constant', constant_values=0)
elif x_diff >0:
out += np.pad(img[-1*y_diff:, :-1*x_diff], ((0,h_pad), (w_pad,0)), 'constant', constant_values=0)
else:
out += np.pad(img[-1*y_diff:, -1*x_diff:], ((0, h_pad), (0,w_pad)), 'constant', constant_values=0)
return np.uint8(out>0)*255
def bi_erosion(img,kernel,ker_center=None):
ker_H, ker_W = kernel.shape
if ker_center == None:
ker_center = np.array([ker_H//2,ker_W//2])
out = np.zeros_like(img)
ker_sum = np.sum(kernel)
img//=np.max(img)
for y in range(ker_H):
for x in range(ker_W):
if kernel[y,x]:
y_diff = ker_center[0]-y
x_diff = ker_center[1]-x
h_pad = abs(y_diff)
w_pad = abs(x_diff)
if y_diff >0 and x_diff >0:
out+=np.pad(img[:-1*y_diff,:-1*x_diff],((h_pad,0),(w_pad,0)),'constant',constant_values=0)
elif y_diff >0:
out += np.pad(img[:-1*y_diff,-1*x_diff:], ((h_pad,0), (0, w_pad)), 'constant', constant_values=0)
elif x_diff >0:
out += np.pad(img[-1*y_diff:, :-1*x_diff], ((0,h_pad), (w_pad,0)), 'constant', constant_values=0)
else:
out += np.pad(img[-1*y_diff:, -1*x_diff:], ((0, h_pad), (0,w_pad)), 'constant', constant_values=0)
return np.uint8(out==ker_sum)*255
구조 요소를 다음과 같이 2개를 선언하고 팽창과 침식한 결과는 다음같다.
struct_small=np.array([[1,1,1]])
struct_big = np.array([[0,1,0],
[1,1,1],
[0,1,0]])
fig =plt.figure(figsize=(13,13))
plt.subplot(321)
plt.imshow(binary_im,cmap='gray')
plt.xlabel('Original')
plt.subplot(323)
plt.imshow(bi_dilation(binary_im,struct_small),cmap='gray')
plt.xlabel('Dilation small')
plt.subplot(324)
plt.imshow(bi_erosion(binary_im,struct_small),cmap='gray')
plt.xlabel('Erosion small')
plt.subplot(325)
plt.imshow(bi_dilation(binary_im,struct_big),cmap='gray')
plt.xlabel('Dilation big')
plt.subplot(326)
plt.imshow(bi_erosion(binary_im,struct_big),cmap='gray')
plt.xlabel('Erosion big')
fig.tight_layout()
plt.show()
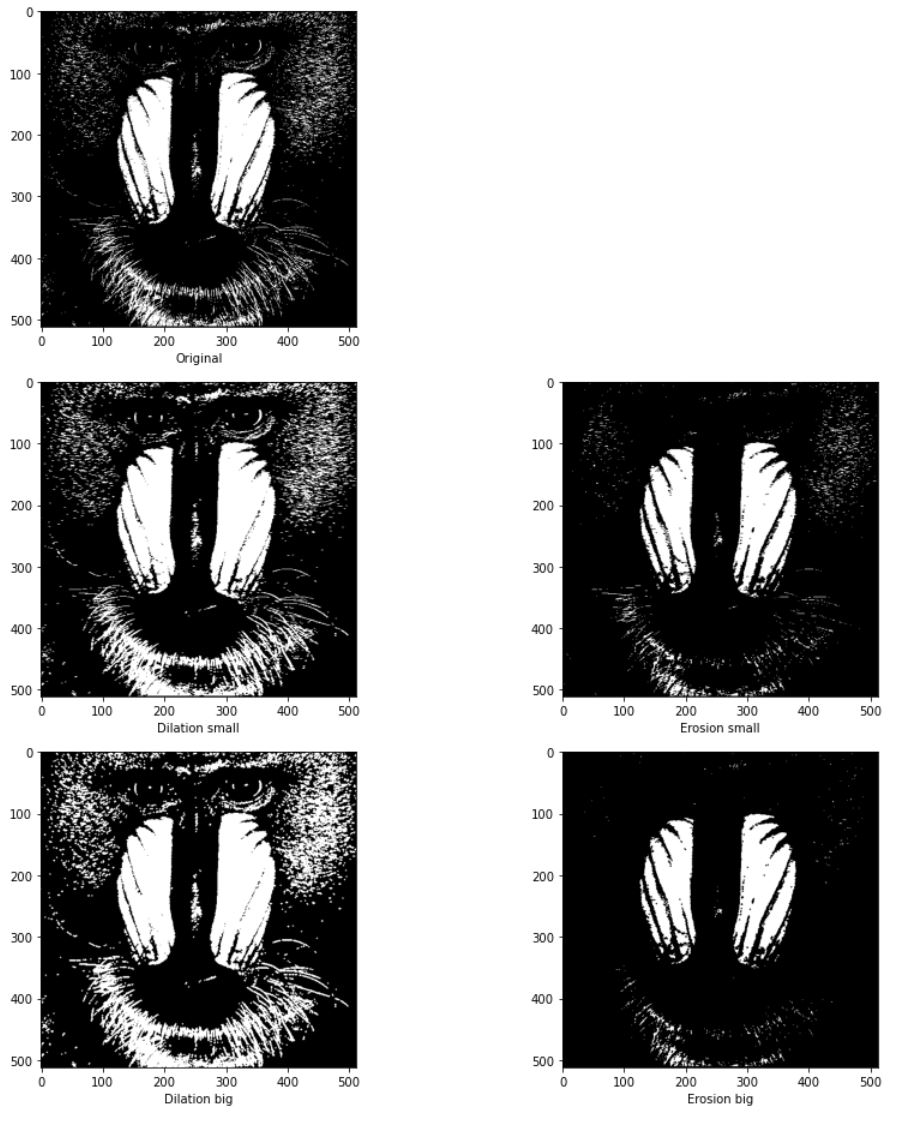
구조요소의 영역에 따라 팽창,침식하는 범위가 바뀌는 것을 확인할 수 있다.
위에서 설명한 바와 같이 일반적으로 명암 모폴로지에서는 kernel의 요소가 0이 되도록 지정한다.
적용한 영상을 보면 다음과 같이 팽창에서는 밝은영역이 커지고 침식에서는 어두운 영역이 늘어난다. 패딩과 영역을 지정하는게 팽창과 침식에서 달라진다. -무한대는 0, 무한대는 255로 설정했다.
def dilation(img,kernel,ker_center=None):
ker_H, ker_W = kernel.shape
H,W,C = img.shape
if ker_center == None:
ker_center = np.array([ker_H//2,ker_W//2])
out = np.zeros([H,W,C,ker_W*ker_H])
count = 0
for y in range(ker_H):
for x in range(ker_W):
y_diff = y-ker_center[0]
x_diff = x-ker_center[1]
h_pad = abs(y_diff)
w_pad = abs(x_diff)
if y_diff >0 and x_diff >0:
out[...,count] = np.pad(img[:-1*y_diff,:-1*x_diff],((h_pad,0),(w_pad,0),(0,0)),'constant',constant_values=0)
elif y_diff >0:
out[...,count] = np.pad(img[:-1*y_diff,-1*x_diff:], ((h_pad,0), (0, w_pad),(0,0)), 'constant', constant_values=0)
elif x_diff >0:
out[...,count] = np.pad(img[-1*y_diff:, :-1*x_diff], ((0,h_pad), (w_pad,0),(0,0)), 'constant', constant_values=0)
else:
out[...,count] = np.pad(img[-1*y_diff:, -1*x_diff:], ((0, h_pad), (0,w_pad),(0,0)), 'constant', constant_values=0)
count+=1
return np.uint8(np.max(out,-1))
def erosion(img,kernel,ker_center=None):
ker_H, ker_W = kernel.shape
H,W,C = img.shape
if ker_center == None:
ker_center = np.array([ker_H//2,ker_W//2])
out = np.zeros([H,W,C,ker_W*ker_H])
count = 0
for y in range(ker_H):
for x in range(ker_W):
y_diff = ker_center[0]-y
x_diff = ker_center[1]-x
h_pad = abs(y_diff)
w_pad = abs(x_diff)
if y_diff >0 and x_diff >0:
out[...,count] = np.pad(img[:-1*y_diff,:-1*x_diff],((h_pad,0),(w_pad,0),(0,0)),'constant',constant_values=255)
elif y_diff >0:
out[...,count] = np.pad(img[:-1*y_diff,-1*x_diff:], ((h_pad,0), (0, w_pad),(0,0)), 'constant', constant_values=255)
elif x_diff >0:
out[...,count] = np.pad(img[-1*y_diff:, :-1*x_diff], ((0,h_pad), (w_pad,0),(0,0)), 'constant', constant_values=255)
else:
out[...,count] = np.pad(img[-1*y_diff:, -1*x_diff:], ((0, h_pad), (0,w_pad),(0,0)), 'constant', constant_values=255)
count+=1
return np.uint8(np.min(out,-1))
ker_small = np.zeros([3,3])
ker_big = np.zeros([5,5])
fig =plt.figure(figsize=(13,13))
plt.subplot(321)
plt.imshow(img)
plt.xlabel('Original')
plt.subplot(323)
plt.imshow(dilation(img,ker_small))
plt.xlabel('Dilation small')
plt.subplot(324)
plt.imshow(erosion(img,ker_small))
plt.xlabel('Erosion small')
plt.subplot(325)
plt.imshow(dilation(img,ker_big))
plt.xlabel('Dilation big')
plt.subplot(326)
plt.imshow(erosion(img,ker_big))
plt.xlabel('Erosion big')
fig.tight_layout()
plt.show()
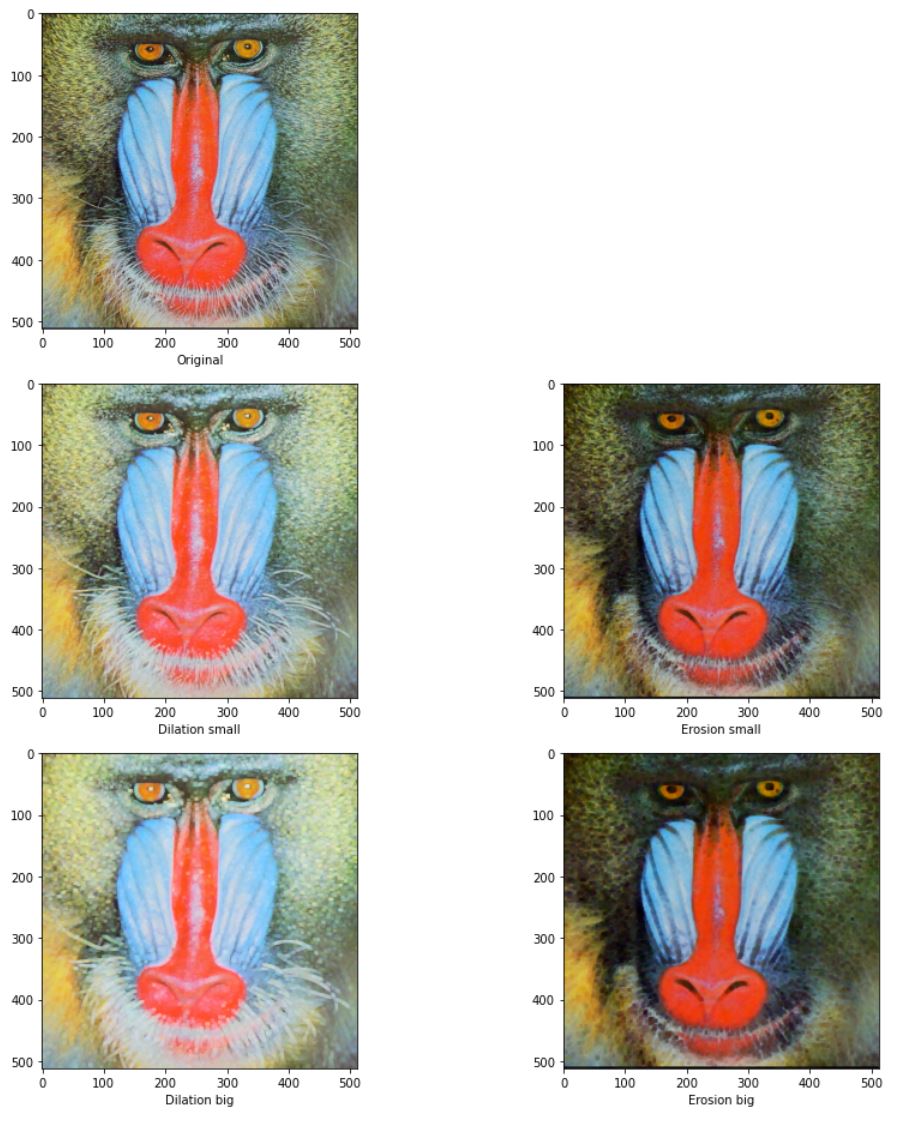
OpenCV
opencv에서는 커널의 값이 0이 아니면 연산을 하는것으로 취급한다.위의 명암 모폴로지 함수에서 이진 모폴로지 처럼 if kernel[y,x]:가 추가되었다고 생각하면 된다.
ker_small = np.ones([3,3])
ker_big = np.ones([5,5])
fig =plt.figure(figsize=(13,13))
plt.subplot(321)
plt.imshow(img)
plt.xlabel('Original')
plt.subplot(323)
plt.imshow(cv2.dilate(img,ker_small))
plt.xlabel('Dilation small')
plt.subplot(324)
plt.imshow(cv2.erode(img,ker_small))
plt.xlabel('Erosion small')
plt.subplot(325)
plt.imshow(cv2.dilate(img,ker_big))
plt.xlabel('Dilation big')
plt.subplot(326)
plt.imshow(cv2.erode(img,ker_big))
plt.xlabel('Erosion big')
fig.tight_layout()
plt.show()
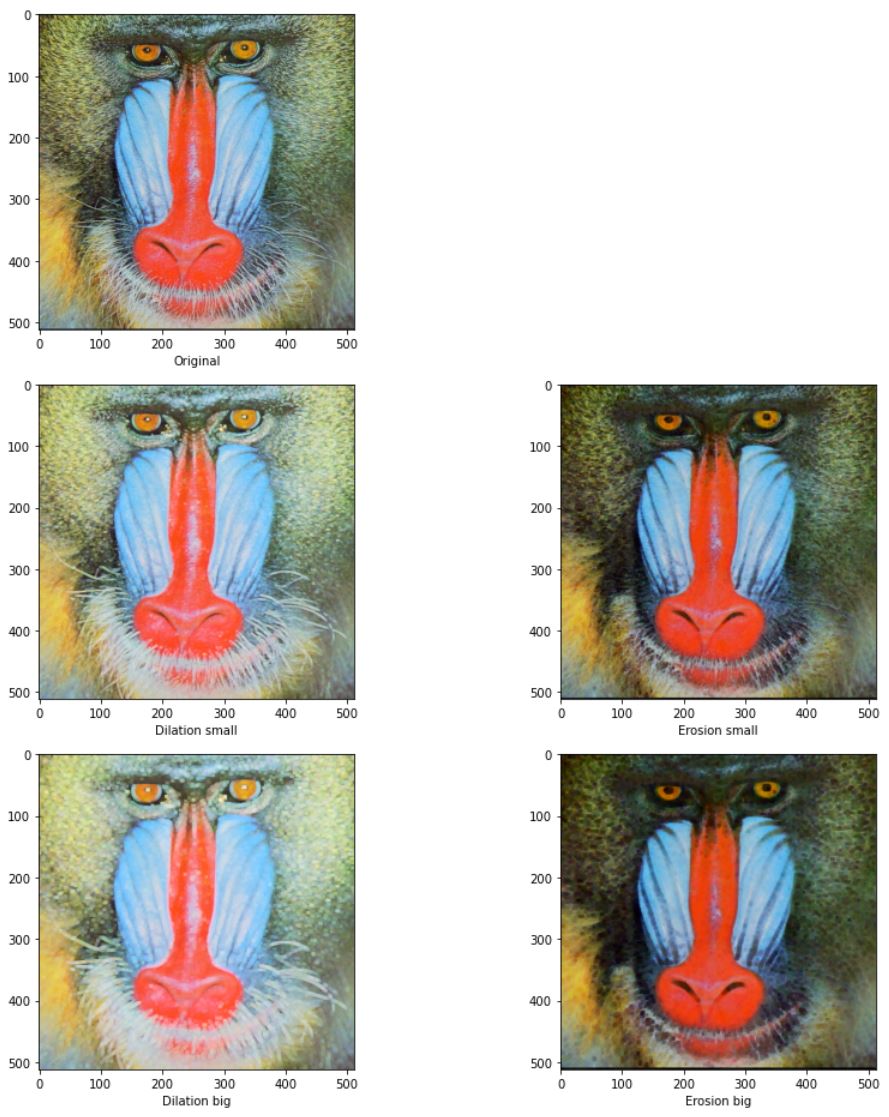
코드링크
영상 피라미드
다해상도

사진 출처
어떤 영상에서는 사람이 영상 전체를 덮을 정도로 크게 나타나기도 하고 반대로 보이지 않을 정도로 아주 작게 나타날 수 있다.
이러한 다양한 상황에서 물체를 안정적으로 찾아내고 인식하는 것이 컴퓨터 비전의 궁극적인 목표 중의 하나이다.
이 문제를 해결하기 위해 고안된 기법중 하나가 영상 피라미드(image pyramid)이다.
영상 피라미드는 여러 해상도의 동일한 이미지 영상으로 구성된다. 큰 해상도부터 작은 해상도까지 쌓아 올린 모양을 보고 피라미드라고 한다. 이를 다중 해상도(multi-resolution) 영상이라 부르기도 한다.
이 구조는 거침과 세밀함(coarse to fine)처리 방식에서 강점을 보이기도 한다. 저해상도의 거친 영상에서 물체의 대략적인 위치와 모양을 찾아낸 후, 고해상도의 세밀한 영상에서 정확한 위치와 모양을 결정하는 접근 방법이다.
피라미드는 샘플링 비율(sampling rate) r을 1/2로 설정해 영상을 절반으로 다운샘플링(down sampling)하는 작업을 반복해 만든다.(이와 반대로 영상의 해상도를 높이는 과정을 업샘플링(up sampling)이라고 한다.)
아래는 피라미드 구성의 식이다.
\[f_{k}(j,i)=f_{k-1}(\frac{j}{r},\frac{i}{r}), r=\frac{1}{2}, 1 \le k \le q\]
q는 몇단계 까지 줄일 것인지를 정한다. 예를들어 1024 X 1024 영상이고 q=6이라면 512 X 512, 256 X 256, 128 X 128, 64 X 64, 32 X 32, 16 X 16과 같이 총 일곱 장의 영상으로 피라미드를 구성할 수 있다.
위 식은 단순하다는 측면에서 좋지만, 에일리어싱이 발생하는 문제를 안고 있다. 이러한 문제는 다운샘플링 과정에서 짝수 좌표의 화소는 100% 참여하는 반면 홀수 좌표의 화소는 0% 참여하기 때문에 발생한다. 참여하지 못하는 화소에도 무시할 수 없는 정보가 들어 있는 것이다.
이러한 문제를 해결하기 위해 버트와 아델슨이 제안한 방식은 다운샘플링을 하기 전에 스무딩을 적용하는 것이다. 이 식은 다섯 화소의 가중치 곱의 합을 계산하는데, 가중치 역할을 하는 스무딩 커널 w 설계가 핵심이다.
\[f_{k}(j,i)= \sum_{y=-2}^{2} \sum_{x=-2}^{2} f_{k-1}(\frac{j}{r}+y,\frac{i}{r}+x), r=\frac{1}{2}, 1 \le k \le q\]
코드 구현
먼저 간단한 다운 샘플링 부터 구현 해보자
새로 만들어진 해상도의 각 픽셀은 원본의 2배의 위치에서 가져오는 방식으로 된다.
import numpy as np
import cv2
import matplotlib.pyplot as plt
def down_simple(img):
out_h,out_w,c = img.shape
out_h//=2
out_w//=2
down_img = np.zeros([out_h,out_w,c],dtype=np.uint8)
for y in range(out_h):
for x in range(out_w):
down_img[y,x] = img[y*2,x*2]
return down_img
사이즈가 16 X 16 아래부터는 형체가 거의 보이지 않으므로 16 X 16 까지만 다운 샘플링을 하도록 범위를 지정해줬다.
img = cv2.cvtColor(cv2.imread('./data/lena.jpg'),cv2.COLOR_BGR2RGB)
min_axis = np.minimum(img.shape[0],img.shape[1])
if np.log2(min_axis) > 4 :
iteration = int(np.log2(min_axis)-4)
else:
iteration = 1
pyramid = []
pyramid.append(img)
subplot_y = (iteration+1)//3 # subplot 지정, 원본도 plot 하기위해 +1, 한 행당 3개의 그림 plot.
if (iteration+1) %3 >0: # 3으로 나눠떨어지지 않으면 행 추가
subplot_y+=1
sub_num = subplot_y*100+31
fig = plt.figure(figsize=(13,13))
plt.subplot(sub_num)
plt.imshow(pyramid[0])
for i in range(iteration):
pyramid.append(down_simple(pyramid[i]))
plt.subplot(sub_num+i+1)
plt.imshow(pyramid[i+1])
fig.tight_layout()
plt.show()

보는 바와 같이 계단현상이 엄청 심하다.
이번에는 버트와 아델슨이 사용한 필터를 사용할 것이다.
smooed_kernel = np.array([[0.0025,0.0125,0.02,0.0125,0.0025],
[0.0125,0.0625,0.1,0.0625,0.0125],
[0.02,0.1,0.16,0.1,0.02],
[0.0125,0.0625,0.1,0.0625,0.0125],
[0.0025,0.0125,0.02,0.0125,0.0025]])
가우시안 커널과 값은 비슷하지만 미세하게 차이가 난다.
>>> gaussian_filter_1d = cv2.getGaussianKernel(5,0)
>>> gaussian_filter_2d = np.outer(gaussian_filter_1d, gaussian_filter_1d.transpose())
>>> print(gaussian_filter_2d)
[[0.00390625 0.015625 0.0234375 0.015625 0.00390625]
[0.015625 0.0625 0.09375 0.0625 0.015625 ]
[0.0234375 0.09375 0.140625 0.09375 0.0234375 ]
[0.015625 0.0625 0.09375 0.0625 0.015625 ]
[0.00390625 0.015625 0.0234375 0.015625 0.00390625]]
컨볼루션 연산을 거치면 해당 픽셀에는 가중치만큼의 값이 되어 있으므로 위의 simple버전에서 스무딩연산만 추가하면 된다.
def smoothing_down(img,kernel):
smooed = cv2.filter2D(img,-1,kernel)
out_h, out_w, c = img.shape
out_h //= 2
out_w //= 2
down_img = np.zeros([out_h, out_w, c], dtype=np.uint8)
for y in range(out_h):
for x in range(out_w):
down_img[y, x] = smooed[y * 2, x * 2]
return down_img
smooed_pyramid = []
smooed_pyramid.append(img)
fig = plt.figure(figsize=(13,13))
plt.subplot(sub_num)
plt.imshow(smooed_pyramid[0])
for i in range(iteration):
smooed_pyramid.append(smoothing_down(smooed_pyramid[i],smooed_kernel))
plt.subplot(sub_num+i+1)
plt.imshow(smooed_pyramid[i+1])
fig.tight_layout()
plt.show()

아주 계단현상이 없다고 할 수는 없지만 확실히 이전보다 나아진것을 볼 수 있다.
커널을 직접 만들지 않고 가우시안 블러를 바로 사용해도 된다.
def gaussian_smoothing_down(img):
smooed = cv2.GaussianBlur(img,(5,5),0)
out_h, out_w, c = img.shape
out_h //= 2
out_w //= 2
down_img = np.zeros([out_h, out_w, c], dtype=np.uint8)
for y in range(out_h):
for x in range(out_w):
down_img[y, x] = smooed[y * 2, x * 2]
return down_img
gaussian_smooed_pyramid = []
gaussian_smooed_pyramid.append(img)
fig = plt.figure(figsize=(13,13))
plt.subplot(sub_num)
plt.imshow(gaussian_smooed_pyramid[0])
for i in range(iteration):
gaussian_smooed_pyramid.append(gaussian_smoothing_down(gaussian_smooed_pyramid[i]))
plt.subplot(sub_num+i+1)
plt.imshow(gaussian_smooed_pyramid[i+1])
fig.tight_layout()
plt.show()

OpenCV
opencv를 사용하게 되면 resize함수를 이용해 다운샘플링, 업샘플링을 수행하게 될것이다.
resize의 interpolation method에도 여러 종류가 있다.
nearst 방식은 가장 단순한 방식이고 area방식은 4x4 영역내의 값을 고려한다.
## opencv resize
# inter_nearest
inter_nearest_pyramid =[]
inter_nearest_pyramid.append(img)
fig = plt.figure(figsize=(13,13))
fig.suptitle("Nearest", fontsize=20)
plt.subplot(sub_num)
plt.imshow(inter_nearest_pyramid[0])
for i in range(iteration):
inter_nearest_pyramid.append(cv2.resize(inter_nearest_pyramid[i],dsize=(0,0),fx=0.5,fy=0.5,interpolation=cv2.INTER_NEAREST))
plt.subplot(sub_num + i + 1)
plt.imshow(inter_nearest_pyramid[i + 1])
fig.tight_layout()
plt.show()
# inter_linear
inter_linear_pyramid =[]
inter_linear_pyramid.append(img)
fig = plt.figure(figsize=(13,13))
fig.suptitle("Linear", fontsize=20)
plt.subplot(sub_num)
plt.imshow(inter_linear_pyramid[0])
for i in range(iteration):
inter_linear_pyramid.append(cv2.resize(inter_linear_pyramid[i],dsize=(0,0),fx=0.5,fy=0.5,interpolation=cv2.INTER_LINEAR))
plt.subplot(sub_num + i + 1)
plt.imshow(inter_linear_pyramid[i + 1])
fig.tight_layout()
plt.show()
# inter_area
inter_area_pyramid =[]
inter_area_pyramid.append(img)
fig = plt.figure(figsize=(13,13))
fig.suptitle("Area", fontsize=20)
plt.subplot(sub_num)
plt.imshow(inter_area_pyramid[0])
for i in range(iteration):
inter_area_pyramid.append(cv2.resize(inter_area_pyramid[i],dsize=(0,0),fx=0.5,fy=0.5,interpolation=cv2.INTER_AREA))
plt.subplot(sub_num + i + 1)
plt.imshow(inter_area_pyramid[i + 1])
fig.tight_layout()
plt.show()
# inter_cubic
inter_cubic_pyramid =[]
inter_cubic_pyramid.append(img)
fig = plt.figure(figsize=(13,13))
fig.suptitle("Cubic", fontsize=20)
plt.subplot(sub_num)
plt.imshow(inter_cubic_pyramid[0])
for i in range(iteration):
inter_cubic_pyramid.append(cv2.resize(inter_cubic_pyramid[i],dsize=(0,0),fx=0.5,fy=0.5,interpolation=cv2.INTER_CUBIC))
plt.subplot(sub_num + i + 1)
plt.imshow(inter_cubic_pyramid[i + 1])
fig.tight_layout()
plt.show()

28 May 2020
•
TIL
27일 : 점연산 구현 다하고 영역연산구현했다. 이후 스터디
28일 : biliteral filter 구현하려다가 실패하고 시간 다보냈다. 결과가 너무 다르다.
구현에 너무 욕심부리지말고 힘들다 싶으면 수식이해하고 빨리 넘어가는게 중요할 것 같다.
핸즈온 머신러닝도 빨리 읽고 싶은데 내일은 아마 시간이 없을 것 같다. ㅠㅠ
TID
TODO list
코드링크
영상처리의 기본 연산
- 영상처리 : 화소 입장에서 봤을 때 새로운 값을 부여받는 것
- 새로운 값을 ‘어디에서’ 취하느냐에 따라 연산이 구분된다
- 점 연산(point operation) : 어떤 화소가 자신의 값만 보고 새로운 값을 결정하는 경우
- 영역 연산(area operation) : 이웃에 있는 몇 개의 화소들을 보고 새로운 값을 정하는 경우
- 기하 연산(geometric operation) : 일정한 기하학적 규칙에 따라 다른 곳에 있는 값을 취하는 경우
점 연산
점 연산의 일반적인 식은 다음과 같다.
\[f_{out}(j,i) = t(f_{1}(j,i),f_{2}(j,i),...,f_{k}(j,i))\]
출력 영상 f_out에서 화소 (j,i)의 값은 k개의 입력 영상에서 같은 위치에 존재하는 화소의 값에 따라 정해진다.
대부분 k=1인 한 장의 영상을 입력한다.
\[f_{out}(j,i) = t(f(j,i)) = \begin{cases} min(f(j,i)+a,L-1), (밝게) \\ max(f(j,i)-a,0), (어둡게) \\ (L-1) - f(j,i), (반전) \end{cases}\]
위의 두 식은 양수 a를 더해서 밝게 만들거나 어둡게 만드는 연산이다.
세 번째 식은 어두운 곳은 밝게 밝은 곳은 어둡게 반전시킨다.
그리고 이들 모두 선형 연산(linear operation)에 속한다.
\[f_{out}(j,i) = (L-1) \times (\hat{f}(j,i))^{\gamma} \\
이때, \hat{f}(j,i) = \frac{f(j,i)}{L-1}\]
위 식은 감마 수정(gamma correction)이라 부르는 비선형 연산(nonlinear operation)으로, \(\hat(f)\)은 [0,1] 사이 값을 갖는 정규 영상이다. 감마 값이 1보다 작으면 밝아지고 1보다 크면 어두워진다. 비선형 연산은 주로 모니터나 프린터의 색상을 조절할 때 사용된다.
점 연산에 속하는 또다른 것으로 히스토그램 평활화를 들 수 있다. 이때는 누적 히스토그램이 변환 함수 역할을 한다.
응용에 따라 맨처음 식에서 영상의 개수 k가 2이상인 경우가 있다. 예를들어, 컬러 영상을 명암 영상으로 변환하는 경우 R, G, B 세 채널이 입력이므로 k=3인 셈이다.
또 다른 경우로 장면 디졸브 (scene dissolve)라는 효과가 있다. 식은 다음과 같이 표현 된다.
\[f_{out}(j,i) = \alpha f_{1}(j,i) + (1-\alpha)f_{2}(j,i)\]
장면 디졸브는 앞의 영상 \(f_{1}\)이 서서히 뒤에 있는 영상 \(f_{2}\)로 전환된다.
점 연산 코드
먼저 선형 연산 부터 실행하면 다음과 같다. 좌측 상단이 원본, 우측 상단이 밝게하는 연산 좌측 하단이 어둡게하는 연산, 우측 하단이 반전 연산이다.
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./data/lena.jpg',cv2.IMREAD_GRAYSCALE)
a = 32
fig = plt.figure()
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.subplot(222)
plt.imshow(np.clip(img+a,0,255),cmap='gray')
plt.subplot(223)
plt.imshow(np.clip(img-a,0,255),cmap='gray')
plt.subplot(224)
plt.imshow(255-img,cmap='gray')
fig.tight_layout()
plt.show()
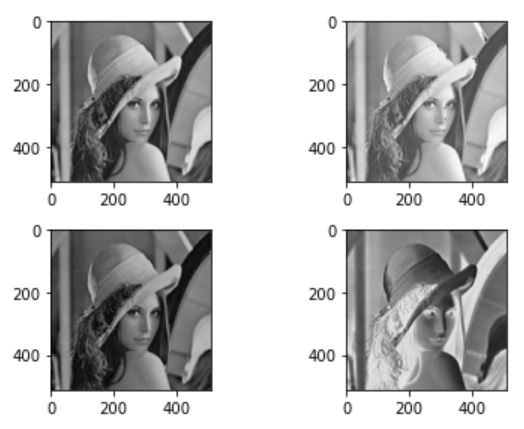
다음은 감마연산(비선형 연산)을 한다. 이를 위해서 함수를 작성할 것이다. 우선 영상을 0~255를 갖는 값을 정규화 해야한다. 그리고 이 이미지의 감마제곱에 다시 255를 곱한다.
def gamma_operation(img,gamma,L):
hat_img = img.copy() / float(L)
return np.clip(L*((hat_img)**gamma),0,L)
fig = plt.figure()
plt.subplot(231)
plt.imshow(img,cmap='gray')
plt.subplot(232)
plt.imshow(gamma_operation(img,0.4,255),cmap='gray')
plt.xlabel('r=0.4')
plt.subplot(233)
plt.imshow(gamma_operation(img,0.67,255),cmap='gray')
plt.xlabel('r=0.67')
plt.subplot(234)
plt.imshow(gamma_operation(img,1.0,255),cmap='gray')
plt.xlabel('r=1.0')
plt.subplot(235)
plt.imshow(gamma_operation(img,1.5,255),cmap='gray')
plt.xlabel('r=1.5')
plt.subplot(236)
plt.imshow(gamma_operation(img,2.5,255),cmap='gray')
plt.xlabel('r=2.5')
fig.tight_layout()
plt.show()
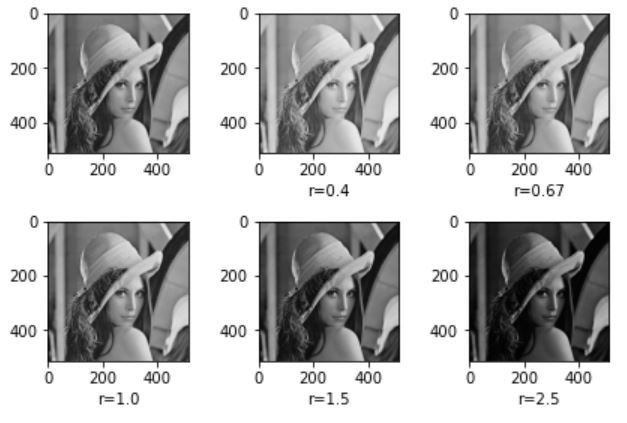
감마 값이 클 수록 이미지가 어두워지고 감마값이 작을 수록 이미지가 밝은 것을 확인 할 수 있다.
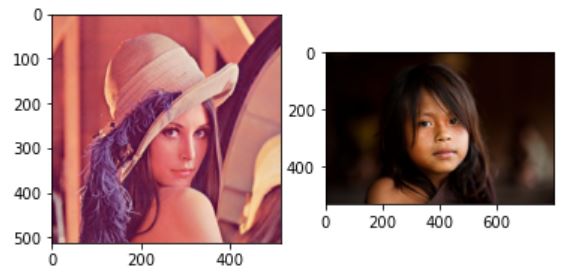
이번에는 디졸브 효과를 구현한다. 먼저 색상영상 두개를 불러온다.
lena = cv2.cvtColor(cv2.imread('./data/lena.jpg'),cv2.COLOR_BGR2RGB)
girl = cv2.cvtColor(cv2.imread('./data/girl.jpg'),cv2.COLOR_BGR2RGB)
plt.subplot(121)
plt.imshow(lena)
plt.subplot(122)
plt.imshow(girl)
plt.show()
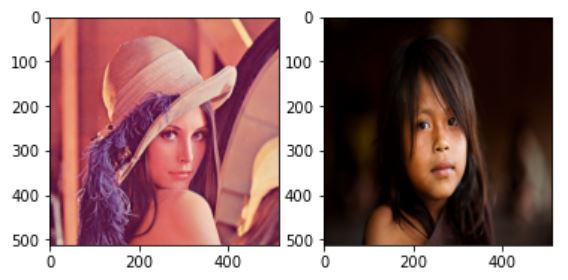
디졸브 효과를 주려면 이미지 두개의 사이즈가 일관되어야 하므로 cv2.resize()를 이용해 크기를 조정해준다.
girl=cv2.resize(girl,lena.shape[:2])
plt.subplot(121)
plt.imshow(lena)
plt.subplot(122)
plt.imshow(girl)
plt.show()
이제 알파값을 1에서 시작해 0까지 내려가며 두 이미지의 가중치를 조절하면 다음과 같이 디졸브 효과가 수행된다. 횟수는 임의로 설정했다.
alpha = 1
leng = 5
step = alpha/leng
fig = plt.figure()
for i in range(6):
n_img = np.uint8(lena*alpha + girl*(1-alpha))
plt.subplot(231+i)
plt.imshow(n_img)
alpha-=step
fig.tight_layout()
plt.show()

영역 연산
다음의 그림은 두 가지 연산인 상관(Correlation)과 컨볼루션(Convolution)에 대한 그림이다.
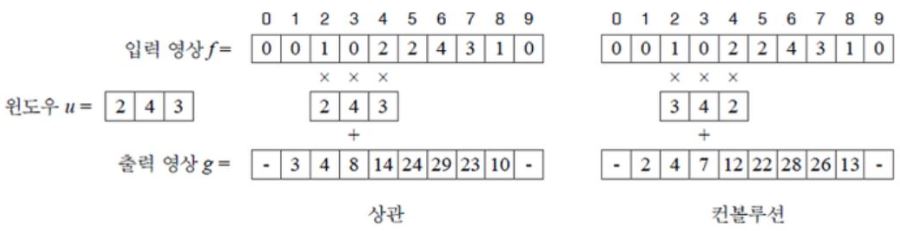
윈도우 u는 검출하려는 물체이고, f는 입력 영상영상이라 할때 풀어야 하는 문제는 f의 어디에 u가 있는지 찾는 것이다.
상관과 컨볼루션
위의 사진에서 영상 g의 값은 6번째 index에서 최대값을 가진다. 이유는 이 위지에 찾고자 하는 u가 있기 때문이다. 반면, u와 많이 다른 곳일수록 낮은 값임을 알 수 있다. 이와 같이, 물체를 표현하는 윈도우 u와 입력 영상 f가 얼마나 비슷한지 측정해 주는 연산을 상관(correlation)이라 부른다. 대표적인 영역 연산이며 물체의 크기나 회전 변환이 없다고 가정한다. 하지만 현실에서는 물체가 크기, 회전, 밝기에서 큰 변화를 나타내기 때문에 제한이 있다.
컨볼루션(convolution)은 상관과 비슷한데, 단지 윈도우를 적용하기 전에 뒤집는 것만 다르다.
연산 도중에 값이 최신화 되면 안되기 때문에 별도의 영상 g에 연산값을 기록해야 한다. 상관과 컨볼루션의 연산을 식으로 표현하면 다음과 같다.
\[1차원 \begin{cases}상관 g(i) = u \otimes f = \underset{x=-(w-1)/2}{\overset{(w-1)/2}{\sum}}u(x)f(i+x) \\
컨볼루션 g(i) = u \circledast f = \underset{x=-(w-1)/2}{\overset{(w-1)/2}{\sum}}u(x)f(i-x)
\end{cases} \\
2차원 \begin{cases}상관 g(j,i) = u \otimes f = \underset{y=-(h-1)/2}{\overset{(h-1)/2}{\sum}} \underset{x=-(w-1)/2}{\overset{(w-1)/w}{\sum}}u(y,x)f(j+y,i+x) \\
컨볼루션 g(j,i) = u \circledast f = \underset{y=-(h-1)/2}{\overset{(h-1)/2}{\sum}} \underset{x=-(w-1)/2}{\overset{(w-1)/w}{\sum}}u(y,x)f(j-y,i-x)
\end{cases}\]
많은 문헌과 연구자들이 상관 대신 컨볼루션이라는 용어를 주로 사용하기 때문에 상관이 컨볼루션으로 불린다. 이 점을 주의하자.
윈도우는 마스크(mask), 커널(kernel), 템플릿(template), 필터(filter)라고도 부른다.
컨볼루션은 일반적인(generic) 연산이다. 컨볼루션 그 자체가 특정 목적이 아니라 마스크의 모양과 크기가 정해지면 그때 비로소 특정 목적이 결정된다. 아래는 널리 사용되는 여러 마스크들의 형태이다.
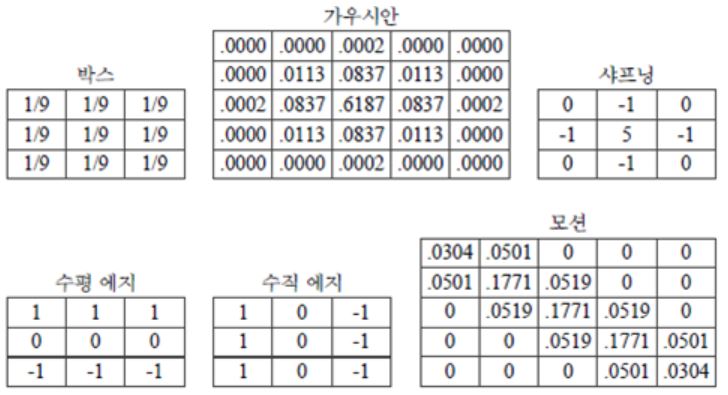 박스 마스크 : 정규 마스크(normalized mask) 라고도 부른다. 마스크의 화소값을 모두 합하면 1이 되도록 정규화를 하기 때문이다. 결과 영상의 화소값이 원래 영상과 비슷한 범위를 가진다.
박스 마스크 : 정규 마스크(normalized mask) 라고도 부른다. 마스크의 화소값을 모두 합하면 1이 되도록 정규화를 하기 때문이다. 결과 영상의 화소값이 원래 영상과 비슷한 범위를 가진다.
가우시안 마스크 : 표준편차가 0.5일 때이다. 박스와 달리 화소로부터 거리에 따라 가중치를 부여한다.
박스나 가우시안과 같은 연산을 스무딩(smoothing) 연산이라 부르며 주로 영상 향상(enhancemant) 작업에 많이 사용한다. 영상의 노이즈는 주로 어떤 화소가 이웃한 화소에 비해 크거나 작은 경우 인데, 스무딩 연산은 이웃 화소끼리의 차이를 줄여 보다 평탄한 영상으로 만들어 주기 때문이다.
샤프닝 : 에지를 뭉개는 스무딩과 반대로 에지를 강조하는 효과를 준다.
에지 마스크 : 일종의 미분 연산자로 영상의 값의 변화를 측정한다. 수평 에지마스크는 y-방향의 미분값, 수직 에지 마스크는 x-방향의 미분값을 측정한다.
모션 : 모션효과를 생성한다.
영역 연산 코드
# 박스
box_filter = np.ones((3,3))/9
# 가우시안
gaussian_filter = np.array([[0.,0.,0.0002,0.,0.],
[0.,0.0113,0.0837,0.0113,0.],
[0.0002,0.0837,0.6187,0.0837,0.0002],
[0.,0.0113,0.0837,0.0113,0.],
[0.,0.,0.0002,0.,0.]])
# 샤프닝
sharpening_filter = np.array([[0,-1,0],
[-1,5,-1],
[0,-1,0]])
# 수평 에지
horizontal_filter = np.array([[1,1,1],
[0,0,0],
[-1,-1,-1]])
# 수직 에지
vertical_filter = np.array([[1,0,-1],
[1,0,-1],
[1,0,-1]])
# 모션
motion_filter = np.array([[0.0304,0.0501,0.,0.,0.],
[0.0501,0.1771,0.0519,0.,0.],
[0.,0.0519,0.1771,0.0519,0.],
[0.,0.,0.0519,0.1771,0.0501],
[0.,0.,0.,0.0501,0.0304]])
각 인덱스마다 행렬 연산을 하면 속도가 꽤 느리다. 이러한 경우 보통 im2col을 사용한다. 코드는 ‘밑바닥부터 시작하는 딥러닝’에서 참고했다.코드 출처
def im2col(input_data, filter_h, filter_w):
H, W, C = input_data.shape
u_pad_h = (filter_h-1)//2
d_pad_h = (filter_h-1)//2
l_pad_w = (filter_w-1)//2
r_pad_w = (filter_w-1)//2
if (filter_h-1) %2 ==1:
u_pad_h +=1
if (filter_w-1)%2 ==1:
l_pad_w +=1
input_data = cv2.copyMakeBorder(input_data, u_pad_h, d_pad_h, l_pad_w, r_pad_w, cv2.BORDER_REPLICATE)
img = np.transpose(input_data,(2,0,1))
col = np.zeros(( C, filter_h, filter_w, H, W))
for y in range(filter_h):
y_max = y + H
for x in range(filter_w):
x_max = x + W
col[:, y, x, :, :] = img[:, y:y_max:1, x:x_max:1]
col = np.transpose(col,(0,3,4,1,2)).reshape(C*H*W, -1)
return col
def conv(img,filter):
filter_h ,filter_w = filter.shape
img_h,img_w,c = img.shape
col = im2col(img,filter_h,filter_w)
col_filetr = filter.reshape((1,-1)).T
out = np.dot(col, col_filetr)
return np.clip(np.transpose(out.reshape((c, img_h, img_w)),(1, 2,0)),0,255)
아래 사진은 각 필터를 적용한 그림이다.
fig = plt.figure(figsize=(13,13))
plt.subplot(331)
plt.imshow(lena)
plt.subplot(334)
box = np.uint8(conv(lena,box_filter))
plt.xlabel("Box")
plt.imshow(box)
plt.subplot(335)
gau = np.uint8(conv(lena,gaussian_filter))
plt.xlabel("Gaussian")
plt.imshow(gau)
plt.subplot(336)
sharp = np.uint8(conv(lena,sharpening_filter))
plt.xlabel("Sharpening")
plt.imshow(sharp)
plt.subplot(337)
hori = np.uint8(conv(lena,horizontal_filter))
plt.xlabel("Horizontal")
plt.imshow(hori)
plt.subplot(338)
veti = np.uint8(conv(lena,vertical_filter))
plt.xlabel("Vertical")
plt.imshow(veti)
plt.subplot(339)
motion = np.uint8(conv(lena,motion_filter))
plt.xlabel("Motion_filter")
plt.imshow(motion)
fig.tight_layout()
plt.show()

opencv에서는 cv2.filter2D 함수를 사용하면 간편하다. 최적화가 이미 잘되어 있기 때문에 속도면에서도 훨씬 빠르다.
fig = plt.figure(figsize=(13,13))
plt.subplot(331)
plt.imshow(lena)
plt.subplot(334)
cv_box = cv2.filter2D(lena,-1,box_filter)
plt.xlabel("Box")
plt.imshow(cv_box)
plt.subplot(335)
cv_gau = cv2.filter2D(lena,-1,gaussian_filter)
plt.xlabel("Gaussian")
plt.imshow(cv_gau)
plt.subplot(336)
cv_sharp = cv2.filter2D(lena,-1,sharpening_filter)
plt.xlabel("Sharpening")
plt.imshow(cv_sharp)
plt.subplot(337)
cv_hori = cv2.filter2D(lena,-1,horizontal_filter)
plt.xlabel("Horizontal")
plt.imshow(cv_hori)
plt.subplot(338)
cv_veti = cv2.filter2D(lena,-1,vertical_filter)
plt.xlabel("Vertical")
plt.imshow(cv_veti)
plt.subplot(339)
cv_motion = cv2.filter2D(lena,-1,motion_filter)
plt.xlabel("Motion_filter")
plt.imshow(cv_motion)
plt.show()
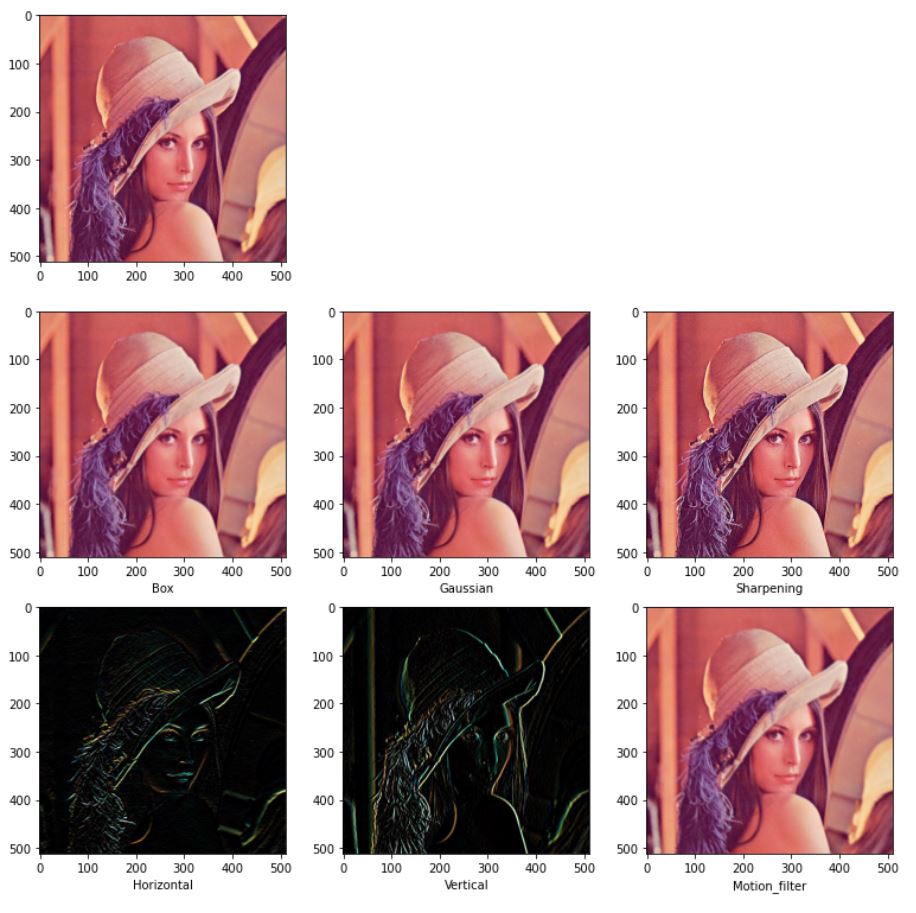
위의 사진을 보면 motion_filter의 커널이 너무 작아 감이 잘 오지 않는다. opencv함수는 최적화가 잘 되어 있으므로 크기가 큰 커널을 사용해도 느리지 않다. 이를 이용해 motion filter를 생성하는 코드를 작성하자 코드는 Stackoverflow에서 참고했다.
def apply_motion_blur(size, angle):
k = np.zeros((size, size), dtype=np.float32)
k[ (size-1)// 2 , :] = np.ones(size, dtype=np.float32)
k = cv2.warpAffine(k, cv2.getRotationMatrix2D( (size / 2 -0.5 , size / 2 -0.5 ) , angle, 1.0), (size, size) )
k = k * ( 1.0 / np.sum(k) )
return k
커널의 사이즈는 51정도로 하고 45도 방향으로 모션을 주면 결과는 다음과 같다.
size = 51
large_motion_filter=apply_motion_blur(size,45)
cv_large_motion = cv2.filter2D(lena,-1,large_motion_filter)
plt.xlabel("Large Motion")
plt.imshow(cv_large_motion)
plt.show()
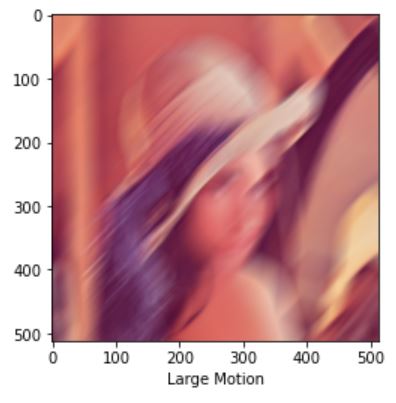
상수를 변수에 곱하고 그것들을 단순히 합하기 때문에 위의 convolution 필터들은 선형이다.
이와 반대로 비선형 연산을 하는 필터들이 있다. 그 중 대표적인 필터가 메디안(median)필터이다. 메디안은 여러 개의 값을 정렬했을 때 가운데 위치한 값을 취한다. 이 필터는 솔트페퍼 잡음(salt-and-pepper noise)제거에 매우 효과적이다.
솔트페퍼 잡음 이미지는 다음과 같이 간단하게 10%의 픽셀을 무작위로 선정해 255값으로 변경했다.
salt_idx = np.random.random(lena.shape[:2])
salt_img = lena.copy()
salt_img[salt_idx>0.9] =255
메디안 필터는 다음과 같이 영역내에서 중간값을 선정했다.
def median(img,filter_size):
img_h,img_w,c = img.shape
pad= (filter_size-1)//2
out_img = np.zeros((img_h,img_w,c))
img = cv2.copyMakeBorder(img, pad, pad, pad, pad, cv2.BORDER_REPLICATE)
img = np.transpose(img,(2,0,1))
for y in range(img_h):
for x in range(img_w):
partial = img[:,y:y+filter_size,x:x+filter_size].reshape(c,-1)
partial.sort()
out_img[y,x]= partial[:,(filter_size**2)//2]
return np.uint8(out_img)
솔트페퍼 잡음이 추가된 이미지에 가우시안 필터를 적용한 결과와 메디안 필터를 적용한 결과는 다음과 같다.
fig = plt.figure(figsize=(13,13))
plt.subplot(221)
plt.imshow(lena)
plt.subplot(222)
plt.imshow(salt_img)
plt.xlabel("salt_and_pepper")
plt.subplot(223)
salt_gaussian = np.uint8(conv(salt_img,gaussian_filter))
plt.imshow(salt_gaussian)
plt.xlabel("gaussian")
plt.subplot(224)
salt_median = median(salt_img,5)
plt.imshow(salt_median)
plt.xlabel("median")
fig.tight_layout()
plt.show()

메디안의 경우 잡음을 많이 제거한 것을 볼 수 있다. 가우시안은 잡음이 덜 제거되었는데, 더 제거하고 싶으면 필터의 크기를 키우면 되지만 이미지의 경계가 뭉개지는 현상이 심해진다. 이러한 특성 때문에 메디안을 에지보존(Edge preseving) 스무딩 필터라 부르기도 한다.
또 다른 유명한 에지보존 스무딩 필터 중 양방향 필터(Bilateral filter)가 있다. 양방향 필터는 두 점 사이의 거리에 대한 가우시안과 두 점의 픽셀 값 차이에 의한 가우시안 값을 고려하는 방식이다. 두 점 사이의 거리에 대한 가우시안은 가우시안 필터와 동일하다. 다른 가우시안 값은 두 점의 픽셀 값 차이가 심한 에지 영역에서 0에 가깝기 때문에 에지 근방에서는 에지가 보존된다.
식은 다음과 같다.
\[g_{p} = \frac{1}{W_p} \sum_{q \in S}G_{\sigma_{s}}(\begin{Vmatrix}p-q \end{Vmatrix})G_{\sigma_r}(\begin{vmatrix}f_{p}-f_{q}\end{vmatrix})f_{q}\]
- f : 입력 영상
- g : 출력 영상
- p, q : 픽셀의 좌표
- G : 표준편차가 \(\sigma\)인 가우시안 분포 함수
- S : 필터 크기
- W : 양방향 필터 마스크 합이 1이 되도록 만드는 정규화 상수
opencv에서 median 필터는 cv2.medianBlur, 양방향 필터는 bilateralFilter 함수를 사용하면 된다.
fig=plt.figure(figsize=(13,13))
plt.subplot(221)
plt.imshow(salt_img)
plt.xlabel("salt")
cv_median_img = cv2.medianBlur(salt_img,5)
plt.subplot(222)
plt.imshow(cv_median_img)
plt.xlabel("median")
plt.subplot(223)
plt.imshow(lena[200:400,200:400])
plt.xlabel("gaussian noise")
cv_bilateral_img = cv2.bilateralFilter(lena[200:400,200:400], 10,12.0,16.0)
plt.subplot(224)
plt.imshow(cv_bilateral_img)
plt.xlabel("bilateral")
fig.tight_layout()
plt.show()

기하연산
기하 연산은 영상을 회전시키거나 특정 영역을 크게 하는 등의 작업이 필요한 경우에 멀리 떨어져 있는 화소의 값들을 이용하는 연산이다.
동차 좌표와 동차 행렬을 이용하면 좀 더 쉽게 연산이 가능하다.
엄연히 말하면 z축이 아니지만 z가 1이고 y와 x는 유지하는 벡터로 표현한다고 생각하면 편하다.
아래 그림 여러 기하연산들의 종류이다.

다음 그림은 전방 변환과 후방 변환에 대한 그림이다.
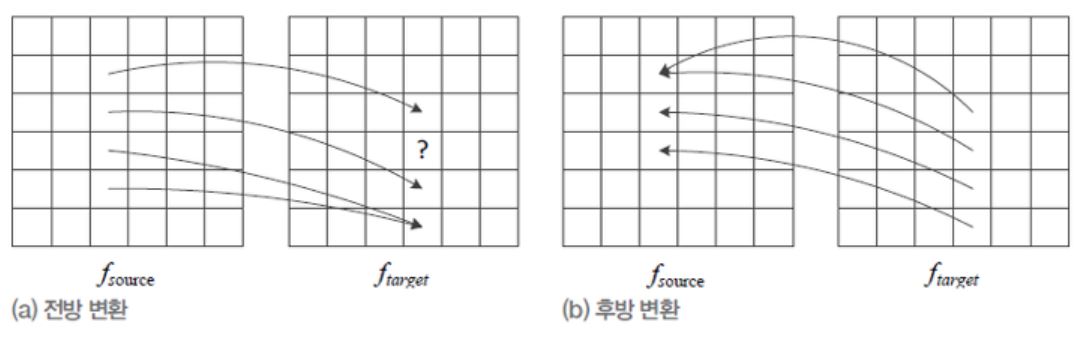 전방 변환은 현재 이미지를 타겟 이미지로 뿌린다고 생각하면 된다. 이때 빈 부분이 생기기 때문에 홀(hole)이 생긴다. 후방 변환은 생성될 이미지의 인덱스에서 현재 이미지 중 해당하는 인덱스를 가져온다고 생각하면 된다.
전방 변환시 홀이 생기거나 후방 변환시 누락되는 이미지 때문에 시각적으로 불만족스러운 현상이 생긴다. 이러한 현상을 에일리어싱(aliasing)이라고 부른다.
또한, 이러한 현상을 해소하려는 노력을 안티 에일리어싱(anti-aliasing)이라고 한다.
전방 변환은 현재 이미지를 타겟 이미지로 뿌린다고 생각하면 된다. 이때 빈 부분이 생기기 때문에 홀(hole)이 생긴다. 후방 변환은 생성될 이미지의 인덱스에서 현재 이미지 중 해당하는 인덱스를 가져온다고 생각하면 된다.
전방 변환시 홀이 생기거나 후방 변환시 누락되는 이미지 때문에 시각적으로 불만족스러운 현상이 생긴다. 이러한 현상을 에일리어싱(aliasing)이라고 부른다.
또한, 이러한 현상을 해소하려는 노력을 안티 에일리어싱(anti-aliasing)이라고 한다.
위의 두 방식에서 실수 좌표를 단순히 반올림하여 정수로 바꾸는데, 목표 영상의 여러 점이 원래 영상의 같은 점을 참조할 수 있으므로 에일리어싱 현상이 남는다. 이러한 문제를 해결하는 효과적인 안티 에일리어싱 기법은 보간(interpolation)이다.
가장 간단한 방식은 반올림하여 정수로 바꾸는 방식은 최근접 이웃(nearest neighbor)방식이라 부른다.
보간법은 정수의 인접 이웃들의 원래 이미지 값들에 거리에 반비례하는 가중치를 주고 이를 합하는 방식이다. 2차원으로 확장하면 다음과 같은 식이 된다.
\[f(y,x')=(1-\alpha)f(y,x)+\alpha f(y,x+1) \\
f(y+1,x') = (1-\alpha)f(y+1,x)+\alpha f(y+1,x+1) \\
f(y',x') = (1-\beta)f(y,x')+\beta f(y+1,x')\]
1차원 상에서만 보간을 수행할 때 선형 보간(linear interpolation)이라 한다.
지금의 경우 y축과 x축 2방향에 대해서 선형 보간이 이루어지기 때문에 양방향 선형보간(bilinear interpolation)방법이라고 한다.
보간 코드 구현
이번에도 역시나 레나로 실험한다.
레나에서 roi를 지정하고 최근접 이웃과 양방향 선형보간을 이용해서 회전변환을 수행할 것이다. 쉽게 구현하기 위해 회전변환의 역행렬을 이용해서 후방 변환을 한다.
참고로 각 인덱스별로 접근하는 방식으로 짜서 시간이 오래걸린다.
gather 함수를 쓰면 좀 더 빠르게 할 수 있다.
def rotation(img,angle,method):
angle = angle /180*np.pi
cos =np.cos(angle)
sin = np.sin(angle)
out = np.zeros_like(img)
if(method=='bilinear'):
for y in range(len(img)):
for x in range(len(img[0])):
x_1 = x-2*cos - y*sin
y_1 = x*sin+y*cos
if x_1<0 or y_1<0 :
continue
if abs(int(x_1+1)-np.clip(int(x_1+1),0,img.shape[0]-1)) >0 or abs(int(y_1+1)-np.clip(int(y_1+1),0,img.shape[1]-1))>1:
continue
alpha = x_1 - int(x_1)
beta = y_1 - int(y_1)
xx = int(x_1)
yy = int(y_1)
if xx == img.shape[1]-1 and yy ==img.shape[0]-1:
out[y,x]=img[yy,xx]
elif xx == img.shape[1]-1:
out[y,x]=img[yy,xx]*(1-beta)+img[yy+1,xx]*beta
elif yy == img.shape[0]-1:
out[y,x]=img[yy,xx]*(1-alpha) + img[yy,xx+1]*alpha
else:
pixel1 = img[yy,xx]*(1-alpha) + img[yy,xx+1]*alpha
pixel2 = img[yy+1,xx]*(1-alpha) + img[yy+1,xx+1]*alpha
out[y,x] = pixel1*(1-beta)+pixel2*beta
elif method == 'nearest':
for y in range(len(img)):
for x in range(len(img)):
x_1 = x * cos - y * sin
y_1 = x * sin + y * cos
if x_1 < 0 or y_1 < 0:
continue
if abs(int(x_1 + 1) - np.clip(int(x_1 + 1), 0, img.shape[0] - 1)) > 0 or abs(
int(y_1 + 1) - np.clip(int(y_1 + 1), 0, img.shape[1] - 1)) > 1:
continue
out[y,x] = img[np.clip(int(y_1+0.5),0,img.shape[1]-1),np.clip(int(x_1 + 0.5), 0, img.shape[0] - 1)]
return out
fig = plt.figure(figsize=(13,13))
plt.subplot(221)
plt.imshow(lena)
roi_resize=lena[200:300,100:200]
plt.subplot(222)
plt.imshow(roi_resize)
plt.subplot(223)
plt.imshow(rotation(roi_resize,10,'nearest'))
plt.xlabel("nearest negihbor")
plt.subplot(224)
plt.imshow(rotation(roi_resize,10,'bilinear'))
plt.xlabel('bilinear interpolation')
fig.tight_layout()
plt.show()

결과에서 최근접 이웃보다 양방향 선형보간 방식의 픽셀이 좀더 자연스러운 것을 볼 수 있다.


















 박스 마스크 : 정규 마스크(normalized mask) 라고도 부른다. 마스크의 화소값을 모두 합하면 1이 되도록 정규화를 하기 때문이다. 결과 영상의 화소값이 원래 영상과 비슷한 범위를 가진다.
박스 마스크 : 정규 마스크(normalized mask) 라고도 부른다. 마스크의 화소값을 모두 합하면 1이 되도록 정규화를 하기 때문이다. 결과 영상의 화소값이 원래 영상과 비슷한 범위를 가진다.





 전방 변환은 현재 이미지를 타겟 이미지로 뿌린다고 생각하면 된다. 이때 빈 부분이 생기기 때문에 홀(hole)이 생긴다. 후방 변환은 생성될 이미지의 인덱스에서 현재 이미지 중 해당하는 인덱스를 가져온다고 생각하면 된다.
전방 변환시 홀이 생기거나 후방 변환시 누락되는 이미지 때문에 시각적으로 불만족스러운 현상이 생긴다. 이러한 현상을 에일리어싱(aliasing)이라고 부른다.
또한, 이러한 현상을 해소하려는 노력을 안티 에일리어싱(anti-aliasing)이라고 한다.
전방 변환은 현재 이미지를 타겟 이미지로 뿌린다고 생각하면 된다. 이때 빈 부분이 생기기 때문에 홀(hole)이 생긴다. 후방 변환은 생성될 이미지의 인덱스에서 현재 이미지 중 해당하는 인덱스를 가져온다고 생각하면 된다.
전방 변환시 홀이 생기거나 후방 변환시 누락되는 이미지 때문에 시각적으로 불만족스러운 현상이 생긴다. 이러한 현상을 에일리어싱(aliasing)이라고 부른다.
또한, 이러한 현상을 해소하려는 노력을 안티 에일리어싱(anti-aliasing)이라고 한다.