Monch

20/05/16~26

26 May 2020 • TIL

구입했던 컴퓨터 비전책을 읽으며 구현해보고 있다. 취업준비 하면서 공부중이라 이전보다 속도가 느려지고 있다. ㅜㅜ 요즘은 기업정보 보다가 하루 다가는거 같다. 프로젝트하는 스터디도 구하고 싶은데 코로나때문인지 구하는 사람들이 많이 안보인다.

TID

2020/05/16 - how to read a paper 정리
2020/05/17~22 프로그래머를 위한 선형대수 필요한 부분만 읽기
2020/05/19 - 코딩테스트 응시
2020/05/23 - 프로그래머를 위한 확률과 통계 1장
2020/05/23~24 - 선형대수 유튜브 강의(이상엽math) 1강~2강
2020/05/23 - 컴퓨터 비전 2-2장
2020/05/24 - 자소서 작성
2020/05/25 - 컴퓨터 비전 2-2장 정리
2020/05/26 - 프로그래머를 위한 확률과 통계 2장-조건부확률까지
2020/05/26 - 컴퓨터 비전 2-3장 공부 및 구현
2020/05/26 - 선형대수 (이상엽math) 3강

TODO list

사진 latex 문법으로 교체 (주말)
매일 종만북-Algospot 1문제 이상 풀기
핸즈온 4장 마무리

벡터공간(VectorSpace)

체(field) $F$에 대한 가군 $(V,+,\cdot)$ 을 벡터공간, $V$의 원소를 벡터라 한다.
이때 $+$는 벡터의 덧셈이고, $\cdot$는 벡터의 Scalar배이다.

(1) 벡터의 공리

$(V,+)$는 아벨군이다 $(u,v,w \in V)$.
- $(u+v)+w=u+(v+w)$.
- $u+v=v+u$.
- $u + \vec{0} = u$ 인 $\vec{0}$가 $V$에 존재한다.
- $u + ( - u ) = \vec{0}$ 인 $-u$가 $V$에 존재한다.
$(V,+,\cdot)$는 $F$의 가군이다. $(k , m \in F)$.
- $k \cdot (m \cdot u) = (km) \cdot u$.
- $F$의 곱셈 항등원 $1$에 대해 $1 \cdot u = u$.
- $(k_m) \cdot (u+v) = k \cdot u + m \cdot u + k \cdot v + m \cdot v$.

(2) 선형 생성(Linear Span)

1) 부분벡터공간

벡터공간 $V$상에서 정의된 덧셈과 스칼라배에 대하여 그 자체로서 벡터공간이 되는 $V$의 부분집합 $W$를 $V$의 부분벡터공간 또는 부분공간이라 한다.

2) 선형생성

벡터공간 $V$의 공집합이 아닌 부분집합 $S={v_{1},v_{2}, \ ... \ ,v_{n}}$ 내의 벡터들의 가능한 모든 선형결합으로 이루어진, $V$의 부분벡터공간을 $S$의 (선형) 생성 $span(S)$이라 한다. 즉, $span(S) = \begin{Bmatrix} \sum_{i=0}^{m} k_{i}v_{i} | \ k_{i} \in F , v_{i} \in S \end{Bmatrix}$ 이때 $S$가 $span(S)$을 (선형)생성한다라고 한다.

ex)

$S=\begin{Bmatrix}(1,0),(0,1)\end{Bmatrix}$. $F=\mathbb{R}$. $\Rightarrow span(S) = \begin{Bmatrix}k(1,0)+m(0,1) \ | \ k,m \in F \end{Bmatrix}$. $= \begin{Bmatrix}k(1,0)+m(0,1) \ | \ k,m \in F \end{Bmatrix}$. $= \mathbb{R^{2}}$.

(3) 선형독립(Linear_independent)

다음을 만족 할 때, 벡터 $a_{1}, ... ,a_{n}$은 선형독립(일차독립 혹은 독립)이라고 한다.
수 $u_{1}, ... , u_{n}$에 대해
$u_{1}a_{1}+...+u_{n}a_{n}=\mathbf{0}$라면
‘$u_{1}=...=u_{n}=0$’
이를 반대로 생각했을 때 벡터(혹은 수의 집합) $x_1 \ne x_2$일 때, $x_{1}-x_{2} \ne 0$이 된다. 즉 결과 $y$에 대한 유일한 표현이 된다.
조건을 만족 못했을때 $a{1}, ... ,a{n}$을 선형종속(일차종속 혹은 종속)이라고 한다.
선형종속이 포함된 사상 $A$는 정방행렬이어도 차원을 감소시키는 사상이 된다.

ex)

$S_{1}=\begin{Bmatrix}(1,0),(0,1),(1,1)\end{Bmatrix}$. $k_{1}(1,0)+k_{2}(0,1)+k_{3}(1,1)=\vec{0}$. $\Rightarrow \left( {k_{1}=k_{2}=k_{3}=0 \\ k_{1}=k_{2}=1 , k_{3}=-1} \right.$. $S_{1}$는 선형종속 집합
$S_{1}=\begin{Bmatrix}(1,0),(0,1)\end{Bmatrix}$. $k_{1}(1,0)+k_{2}(0,1)=\vec{0}$. $\Rightarrow k_{1}=k_{2}=0$._ $$S_{2}는 선형독립 집합

(4) 여러 벡터공간

1) 노름공간(Norm space)

노름이 부여된 $K-$벡터공간 $(V,\begin{Vmatrix} \cdot \end{Vmatrix})$
노름이란 $\forall u, v \in V, \forall k \in K$에 대해 아래 세 조건을 만족시키는 함수
$\begin{Vmatrix} \cdot \end{Vmatrix}: V \rightarrow [0, \infin)$이다. $(K \in \begin{Bmatrix}R,C\end{Bmatrix} )$, 여기서 $R$은 실수집합 $C$는 복소수집합.

$\begin{Vmatrix} kv \end{Vmatrix} = \begin{vmatrix} k \end{vmatrix} \begin{Vmatrix} v \end{Vmatrix}$.
$\begin{Vmatrix} u+v \end{Vmatrix} \leqq \begin{Vmatrix} u \end{Vmatrix} + \begin{Vmatrix} v \end{Vmatrix}$.
$\begin{Vmatrix} v \end{Vmatrix} = 0 \Leftrightarrow v= \vec{0}$.

2) 내적공간

내적이 부여된 $K-$벡터공간 $(V,\left\langle \cdot,\cdot \right\rangle)$.
내적이란 $\forall u, v, w \in V, \forall k \in K$에 대해 아래 네 조건을 만족시키는 함수 $\left\langle \cdot,\cdot \right\rangle : V \times V \rightarrow K$이다. $(K\in \left\{ {R,C} \right\})$.

$\left\langle u+v,w \right\rangle = \left\langle u,w \right\rangle + \left\langle u,w \right\rangle$.
$\left\langle ku,v \right\rangle = k\left\langle v,u \right\rangle$.
$\left\langle u,v \right\rangle = \left\langle \overline{v,u} \right\rangle$.
$v \neq \vec{0} \Rightarrow \left\langle v,v \right\rangle > 0$.

3) 유클리드 공간

음이 아닌 정수 $n$에 대하여 $n$차원 유클리드공간 $\mathbb{R^{n}}$은 실수집합 $\mathbb{R}$의 $n$번 곱집합이며, 이를 $n$차원 실수 벡터공간으로써 정의하기도 한다. 내적 $\left\langle u,v \right\rangle=\sum_{i=1}^{n}u_{i}v_{i}=u \cdot v$을 정의하면 점곱, 스칼라곱 이라고도한다.

4) 기저와 차원

1 - 기저
벡터공간 $V$의 부분집합 $B$가 선형독립이고 $V$를 생성할 때, $B$를 V의 기저라 한다.

ex)

$B_{1} = \left\{ (1,0) ,(0,1)\right\}$. $\Rightarrow span(B_{1}) = \mathbb{R^2}$.
따라서 $B_{1}$은 $V$의 기저이다.
$B_{2} = \left\{ (1,0) ,(1,1) \right\}$. $(a,b) = k(1,0)+m(1,1) = (k+m,m)$._ $m=b, k=a-b$.
따라서 $B_{2}$는 $V$의 기저이다.
$S= \left\{ (1,0), (0,1) , (1,1)\right\}$. $span(S) = \mathbb{R^2}$.
성립하지만 선형종속이다. 따라서 $S$는 $V$의 기저가 아니다.

2 - 차원
$B$가 벡터공간 $V$의 기저일 때 $B$의 원소의 개수를 $V$의 차원 $dim(V)$라 한다.

ex)

기저의 예제에서 $dim(V)=n(B_{1})=n(B_{2})=2$.

3 - 정규기저
다음 조건을 만족하는 노름공간 $V$의 기저 $B$를 정규기저라 한다. $\forall b \in B, \begin{Vmatrix}b\end{Vmatrix}=1$

4 - 직교기저
다음 조건을 만족하는 내적공간 $V$의 기저 $B$를 직교기저라 한다. $\forall b_{1},b_{2} \in B, \left\langle b_{1},b_{2} \right\rangle =0$

5 - 정규직교기저
정규기저이자 직교기저인 내적공간의 기저를 정규직교기저라 한다.
특히 $\mathbb{R^{n}}$의 정규직교기저 $$\left{ (1,0,…,0),(0,1,…,0),(0,0,…,1) \right}를 표준기저라 한다.

ex)

$\mathbb{R^2}$에 대해서

$B_{1}= \left\{ (2,0),(1,1) \right\}$ 정규 X, 직교 X
$B_{2}= \left\{ (1,0),(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) \right\}$ 정규 O, 직교 X
$B_{3}= \left\{ (1,1),(1,-1) \right\}$ 정규 X, 직교 O
$B_{4}= \left\{ (1,0),(0,1) \right\}$ 정규 O, 직교 O

대수구조

26 May 2020 • Linear Algebra

대수구조(Algebraic Structure)

대수 : 수를 대신한다.

수 뿐 아니라 수를 대신할 수 있는 모든 것을 대상으로 하는 집합과 그 집합에 부여된 연산이 여러 가지 공리로써 엮인 수학적 대상.
간단히 일련의 연산들이 주어진 집합을 대수구조라고 한다.

여러 대수구조

반군 : 집합과 그 위의 결합법칙을 따르는 하나의 이항 연산을 갖춘 대수구조
모노이드 : 항등원을 갖는 반군
군(group) : 역원을 갖는 모노이드 (집합, 이항연산 하나, 결합법칙, 항등원, 역원을 갖춰야 한다.)
아벨군(abelian group,또는 가환군(commutative group)) : 교환법칙이 성립하는 군
환(ring) : 덧셈에 대하여 아벨군, 곱셈에 대하여 반군(결합법칙)을 이루고 분배법칙이 성립하는 대수구조
ex) A가 정수 집합, (A, +, x)의 경우 +가 아벨군, x가 반군(정수 공간에서 소수가 포함되지 않아 역원 존재하지 않음) 이때 대수구조 (A, +, x)는 환이다.
가군(module) : 어떤 환의 원소에 대한 곱셈이 주어지며, 분배법칙이 성립하는 아벨군
ex) 벡터공간
가환환(commutative ring 또는 비가환체(skew field)) : 겁셈이 교환법칙을 만족하는 환
나눗셈환(division ring) : 0이 아닌 모든 원소가 역원(=항등원을 가진다)을 가지며, 원소의 개수가 둘 이상인 환
체(field) : 가환환인 나눗셈환. 즉, 사칙연산이 자유로이 시행 될 수 있고 산술의 잘 알려진 규칙들을 만족하는 대수구조
ex) 유리수, 실수, 복소수의 연산

범람 채움(Flood_fill)

26 May 2020 • Computer Vision

범람 채움(Flood_fill)

연결요소의 크기를 어느정도로 하느냐에 따라 다르다.
일반적으로 상하좌우(4-연결성),사각형(8-연결성) 등을 사용한다.
이 크기만큼 연결되어 있을 때 집합 각각을 연결요소(Connected component)라고 한다. 그리고 이 연결요소들에 번호를 부여한 것을 범람 채움(Flood fill)이라고 한다.

코드구현

코드링크

이번에도 레나로 시작한다. OpenCV의 INV flag를 써서 -1을 빼거나 그냥 BINARY flag를 사용해서 X-1로 해도 된다. 이진화 영상에서 나타난 부분을 -1로 하는게 포인트이다.
이번에는 레나사진에서 히스토그램을 추출하고 여기서 값을 정해 이진화를 진행할 것이다.

import numpy as np
import cv2
import matplotlib.pyplot as plt
import queue

img = cv2.imread('./data/lena.jpg',cv2.IMREAD_GRAYSCALE)
ret,thr = cv2.threshold(img,200,255,cv2.THRESH_BINARY_INV)

flood = thr.copy()/255.
flood -=1
plt.imshow(flood.copy()*-1,cmap='gray')
plt.show()

단순 이중 for문을 돌면서 DFS로 탐색하면 재귀 호출이 깊어져 스택 오버플로우가 발생할수 있기 때문에 queue를 이용해서 함수를 작성하고 연결요소마다 번호를 부여한다.

def flood_fill(img,j,i,label):
    q = queue.Queue()
    q.put((j,i))
    while q.qsize():
        (y,x)= q.get()
        if img[y,x] == -1:
            left=right=x
            while left-1>0 and img[y,left-1] == -1:
                left-=1
            while right+1<img.shape[1] and img[y,right+1] ==-1:
                right+=1
            for z in range(left,right+1):
                img[y,z]=label
                if y-1>0 and img[y-1,z]==-1 and (z==left or (z-1>0 and img[y-1][z-1] !=-1)):
                    q.put((y-1,z))
                if y+1<img.shape[1] and img[y+1,z]==-1 and (z==left or (z-1>0 and img[y+1][z-1] !=-1)):
                    q.put((y+1,z))


label = 1
for j in range(img.shape[0]):
    for i in range(img.shape[1]):
        if(flood[j,i]==-1):
            flood_fill(flood,j,i,label)
            label+=1

실제 확인을 하고 싶으면 다음과 같이 하면 된다. 연결요소가 너무 짧은 경우 점조차 보기 힘들다.

floos = np.zeros((img.shape[0],img.shape[1],label))
for i in range(1,label+1): # label은 1부터 시작하므로 주의한다.
    floos[...,i-1] = flood == i
floos = floos.astype(np.float32)

for i in range(label):
    plt.imshow(floos[...,i],cmap='gray')
    plt.show()

영상 이진화(Binarization)

26 May 2020 • Computer Vision

영상 이진화

어떠한 기준 T로 명암값을 흑과 백 하나로 결정하는 방법이다. 이때 기준 T를 임계값(Threshold)라고 한다.
일반적인 식은 다음과 같다.

\[b(j,i) = \begin{cases}1, f(j,i) \ge T \\ 0, f(j,i) < T \end{cases}\]

이번에는 레나사진에서 히스토그램을 추출하고 여기서 값을 정해 이진화를 진행할 것이다.

import cv2
import matplotlib.pyplot as plt
import numpy as np

img = cv2.imread('./data/lena.jpg',cv2.IMREAD_GRAYSCALE)

hist = np.zeros(256)
img_flat = np.reshape(img,-1)
for i in range(len(img_flat)):
    hist[img_flat[i]]+=1
hist = hist/len(img_flat)

fig = plt.figure()
plt.subplot(121)
plt.imshow(img,cmap='gray')
plt.subplot(122)
plt.bar(np.arange(256),hist)
plt.xlim([0,256])
fig.tight_layout()
plt.show()

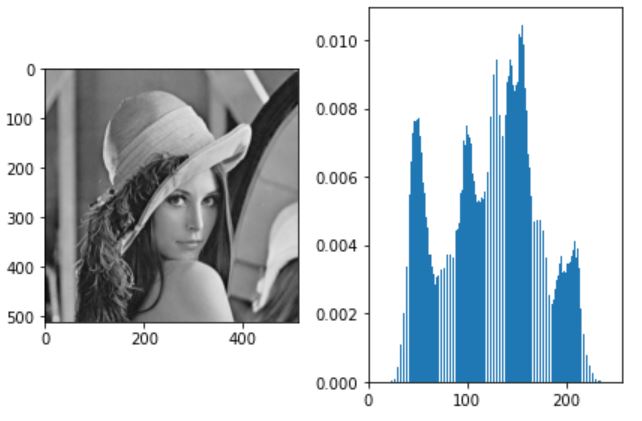
분포가 최대한 고른 지점은 약 120정도로 보인다. 따라서 120을 임계값으로 이진화를 진행한다.

def Threshold(img, T):
    return np.uint8(img>T)*255

bi_img = Threshold(img,120)

plt.imshow(bi_img,cmap='gray')
plt.show()

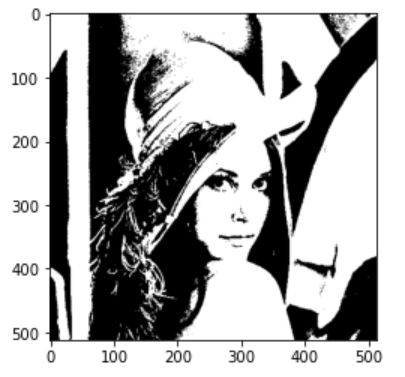
임계값 방법은 단순한 반면 이렇게 히스토그램을 관찰하여 해야하지만 컴퓨터 비전에서는 이것을 자동화 해야한다. 히스토그램의 봉우리 부분이 뚜렸하지 않을 수록 임계값을 콕 집어내기 애매한 경우가 많다.

오츄알고리즘 (Otsu Algoritm)

오츄가 제안한 알고리즘은 현재도 널리 사용되는 이진화 알고리즘이다. 임계값 $t$를 기준으로 화소를 두 집합으로 나누었을 때, 각 집합의 명암 분포가 균일할수록 좋다는 점에 착안해 균일성이 클수록 $t$에게 높은 점수를 준다. 균일성은 그룹의 분산으로 측정하고 분산이 작을수록 균일성이 높다. 가능한 $t$에 대해 점수를 계산한 후 가장 좋은 $t$를 최종 임계값으로 취한다. 일종의 최적화 알고리즘이다.
여기서 목적 함수(Objective function) 혹은 비용 함수(Cost function)은 분산을 사용한다. 분산이 작을수록 균일성이 크므로 목적 함수값이 작을수록 점수가 높다고 거꾸로 생각해야 한다.
식은 다음과같다. $T = \underset{t \in \left\{ 0,1,...,L-1 \right\}}{argmin} v_{within}(t) \\ v_{within}(t) = w_{0}(t)v_{0}(t) + w_{1}(t)v_{1}(t) \\ w_{0}(t) = \sum_{i=0}^{t} \hat{h}(i), \qquad w_{1}(t) = \sum_{i=t+1}^{L-1} \hat{h}(i) \\ \mu_{0}(t) = \frac{1}{w_{0}(t)} \sum_{i=0}^{t} i \hat{h}(i), \qquad \mu_{1}(t) = \frac{1}{w_{1}(t)} \sum_{i=t+1}^{L-1} i \hat{h}(i) \\ v_{0}(t) = \frac{1}{w_{0}(t)} \sum_{i=0}^{t} \hat{h}(i)(i-\mu_{0}(t))^{2}, \qquad v_{1}(t) = \frac{1}{w_{1}(t)} \sum_{i=t+1}^{L-1} \hat{h}(i)(i-\mu_{1}(t))^{2}$

여기서 $v_{within}(t)$ 가 목적 함수 역할을 하고 두 분산의 가중치 합으로 정의된다. $w_{0}(t)$와 $w_{1}(t)$는 임계값 $t$에 따라 생성된 흑 화소와 백 화소 집합의 크기로서 가중치 역할을 한다. $v_{0}(t)$와 $v_{1}(t)$는 두 집합의 분산이다. $\mu$는 평균값이다.
여기서 두 개의 가중치와 두 개의 분산을 L번 계산해야 하므로 알고리즘의 점근적 시간 복잡도(asymptotic time complexity)는 $O(L^2)$이다. 따라서 실시간 처리에서는 부담스럽다.
개선하기 위해 먼저 $\mu$와 $v$는 주어진 영상에 대해 한 번만 계산하면 되기 떄문에 상수로 간주 가능하다.
$\mu = \sum_{i=0}^{L-1}i\hat{h}(i), \ v=\sum_{i=0}^{L-1}(i-\mu)^2\hat{h}(i)$

이 식은 다음과 같이 쓸 수 있다.
$v = \sum_{i=0}^{t}(i-\mu_{0}(t)+\mu_{0}(t)-\mu)^2\hat{h}(i) + \sum_{i=t+1}^{L-1}(i-\mu_{1}(t)+\mu_{1}(t)-\mu)^2\hat{h}(i) \\ = \sum_{i=0}^{t}((i-\mu_{0}(t))^2 + 2(i-\mu_{0}(t))(\mu_{0}(t)-\mu)+(\mu_{0}(t)-\mu)^2)\hat{h}(i)+ \\ \sum_{i=t+1}^{L-1}((i-\mu_{1}(t))^2+2(i-\mu_{1}(t))(\mu_{1}(t)-\mu)+(\mu_{1}(t)-\mu)^2)\hat{h}(i)\\ = \sum_{i=0}^{t}((i-\mu_{0}(t))^2 + (\mu_{0}(t)-\mu)^2)\hat{h}(i) + \sum_{i=t+1}^{L-1}((i-\mu_{1}(t))^2+(\mu_{1}(t)-\mu)^2)\hat{h}(i)$ 이전 식에 다시 대입하면
$v=\left\{ w_{0}(t)(\mu_{0}(t)-\mu)^2 + w_{1}(t)(\mu_{1}(t)-\mu)^2\right\} + \sum_{i=0}^{t}(i-\mu_{0}(t))^2\hat{h}(i)+\sum_{i=t+1}^{L-1}(i-\mu_{1}(t))^2\hat{h}(i) \\ = \left\{ w_{0}(t)(\mu_{0}(t)-\mu)^2 + w_{1}(t)(\mu_{1}(t)-\mu)^2\right\} + \left\{ w_{0}(t)v_{0}(t)+w_{1}(t)v_{1}(t)\right\}$ $w_{1}(t) = 1- w_{0}(t)$와 $\mu = w_{0}(t) \mu_{0}(t) + w_{1}(t) \mu_{1}(t)$를 대입해 정리하면 (사실 이 부분 이해가 안간다) $v = w_{0}(t)(1-w_{0}(t))(\mu_{0}(t)-\mu_{1}(t))^2 + v_{within}(t) = v_{between}(t)+v_{within}(t)$ $v$는 상수 이므로 $v_{within}(t)$를 최소화하는 일은 $v_{between}(t)$를 최대화하는 것과 똑같다. 따라서 최대화 문제를 다음과 같이 바꿀 수 있다. $T = \underset{t \in \left\{ 0,1,...,L-1 \right\}}{argmin} v_{between}(t) \\ where, v_{between}(t) = w_{0}(t)(1-w_{0}(t))(\mu_{0}(t)-\mu_{1}(t))^2$ 전체적인 수식은 다음과 같이 쓸 수 있다. $초깃값 (t=0) : w_{0}(0)=\hat{h}(0), \mu_{0}(0)=0 \\ 순환식(t>0) : \\ w_{0}(t)=w_{0}(t-1)+\hat{h}(t)\\ \mu_{0}(t) = \frac{w_{0}(t-1)\mu_{0}(t-1)+t\hat{h}(t)}{w_{0}(t)}\\ \mu_{1}(t) = \frac{\mu - w_{0}(t)\mu_{0}(t)}{1-w_{0}(t)}$ 과정 이해가 잘 안가므로 컨셉만 외워야 겠다.

코드 구현

코드링크

위에서 이진화로 이미 정규화된 히스토그램을 그렸다. 위 코드에서 이어서 구현을 한다. 먼저 $\mu$를 구하고 나머지 값들을 초기화해 준다.

mu = 0

for i in range(256):
    mu+= i*hist[i]
    
w =np.zeros(256)
mu0 =np.zeros(256)
mu1 =np.zeros(256)
T_bet =0
w[0] = hist[0]
threshold=0

순환식을 따라 T_bet 값이 최대값일때마다 threshold 값을 index값으로 변경한다.

for i in range(1,256):
    w[i] = w[i-1]+hist[i]
    mu0[i] = (w[i-1]*mu0[i-1]+i*hist[i])/(w[i]+1e-10)
    mu1[i] = (mu - w[i]*mu0[i])/(1-w[i]+1e-10)
    n_t = w[i]*(1-w[i])*((mu0[i]-mu1[i])**2)

    if n_t>T_bet:
        T_bet = n_t
        threshold = i

이제 이 threshold 값으로 이진화를 진행하면 끝이다.

otsu_img = Threshold(img,threshold)

plt.imshow(otsu_img,cmap='gray')
plt.show()

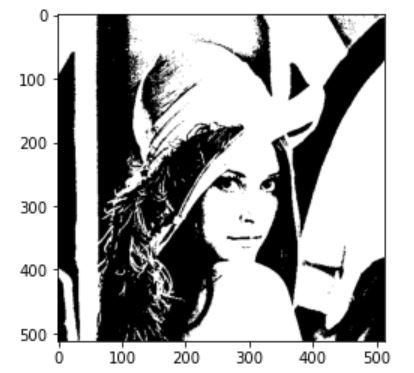
OpenCV

opencv에서는 cv2.threshold 함수를 사용하면 가능하다. 각 flag마다 method가 살짝씩 다르게 작동한다. otsu는 따로 작용하는게 아니라 thr6과 같이 입력해야 한다.

ret, thr = cv2.threshold(img,120,255,cv2.THRESH_BINARY)
ret2, thr2 = cv2.threshold(img,120,255,cv2.THRESH_BINARY_INV)
ret3, thr3 = cv2.threshold(img,120,255,cv2.THRESH_TRUNC) # 픽셀값이 임계값 보다 크면 임계값, 작으면 픽셀값 그대로
ret4, thr4 = cv2.threshold(img,120,255,cv2.THRESH_TOZERO) # 픽셀값이 임계값 보다 크면 픽셀 값 그대로, 작으면 0
ret5, thr5 = cv2.threshold(img,120,255,cv2.THRESH_TOZERO_INV) # 픽셀값이 임계값 보다 크면 0, 작으면 픽셀값 그대로
ret6, thr6 = cv2.threshold(img,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)

fig = plt.figure()
plt.subplot(231)
plt.imshow(thr,cmap='gray')
plt.subplot(232)
plt.imshow(thr2,cmap='gray')
plt.subplot(233)
plt.imshow(thr3,cmap='gray')
plt.subplot(234)
plt.imshow(thr4,cmap='gray')
plt.subplot(235)
plt.imshow(thr5,cmap='gray')
plt.subplot(236)
plt.imshow(thr6,cmap='gray')
fig.tight_layout()
plt.show()

Older