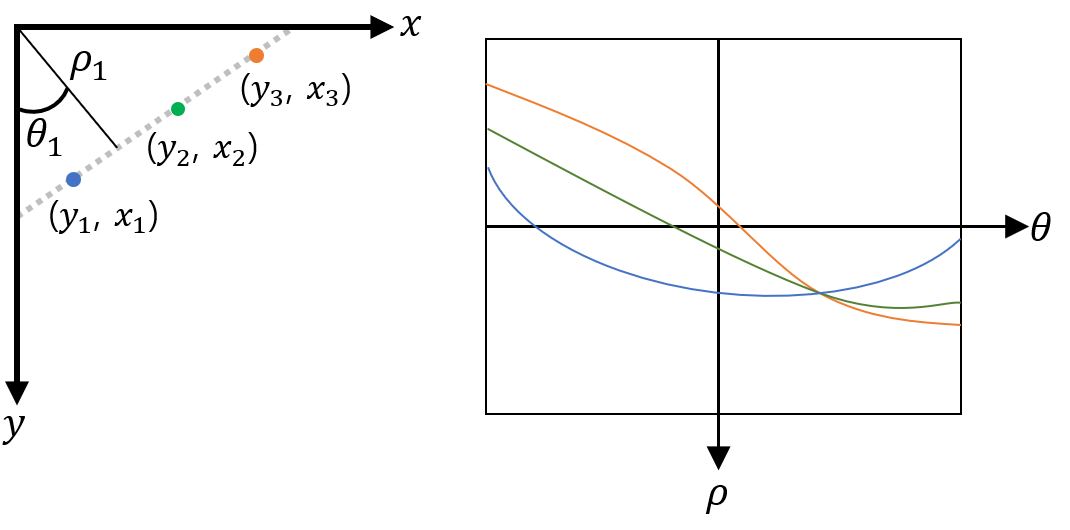
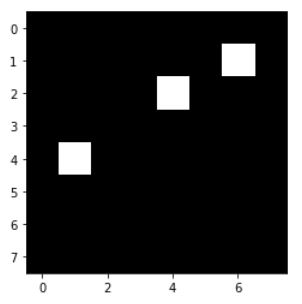
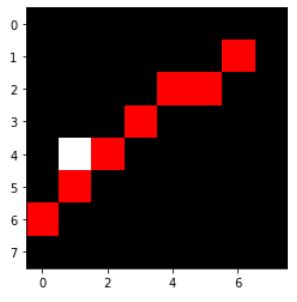
def edge_segment_detection(spta_img):
dx = np.array([0, 1, 1, 1, 0, -1, -1, -1])
dy = np.array([1, 1, 0, -1, -1, -1, 0, 1])
spta_img[0, :] = spta_img[:, 0] = spta_img[-1, :] = spta_img[:, -1] = 0
spta_img //=255
c = np.zeros_like(spta_img)
## 전환횟수 체크
for i in range(1, len(spta_img) - 1):
for j in range(1, len(spta_img[0]) - 1):
flag = False
count = 0
for z in range(9):
idx = z
if z == 8:
idx = 0
y = i + dy[idx]
x = j + dx[idx]
if flag and spta_img[y, x] == 0:
count += 1
flag=False
elif spta_img[y, x]:
flag = True
else:
flag=False
c[i, j] = count
zeros = np.zeros([spta_img.shape[0], spta_img.shape[1], 3], np.uint8)
# start and branch, red = start or end point, blue = branch
zeros[..., 0] = spta_img * 255
zeros[..., 1] = spta_img * 255
zeros[..., 2] = spta_img * 255
zeros[..., 1] = np.where(c == 1, 0, zeros[..., 1])
zeros[..., 2] = np.where(c == 1, 0, zeros[..., 2])
zeros[..., 0] = np.where(c >= 3, 0, zeros[..., 0])
zeros[..., 1] = np.where(c >= 3, 0, zeros[..., 1])
plt.imshow(zeros)
plt.xlabel("start")
plt.show()
# 끝점 혹은 분기점 입력
Q = queue.Queue()
for i in range(1, len(spta_img) - 1):
for j in range(1, len(spta_img[0]) - 1):
if c[i, j] == 1 or c[i, j] >= 3:
for z in range(8):
y = dy[z] + i
x = dx[z] + j
if spta_img[y, x]:
Q.put((i, j, z))
n = 0
visited = np.zeros_like(spta_img)
segment = []
while not Q.empty():
(y, x, dir) = Q.get()
cy = dy[dir] + y
cx = dx[dir] + x
if visited[cy, cx]:
continue
n += 1
n_seg = []
n_seg.append([y, x])
n_seg.append([cy, cx])
visited[y, x] = visited[cy, cx] = 1
if c[cy, cx] == 1 or c[cy, cx] >= 3:
continue
while True:
flag = False
fronts = front_pixel(cy, cx, dir)
for f in fronts:
n_y, n_x, n_dir = f
if c[n_y, n_x] == 1 or c[n_y, n_x] >= 3:
flag = True
visited[n_y, n_x] = 1
n_seg.append([n_y, n_x])
break
if flag:
break
else:
for f in fronts:
n_y, n_x, n_dir = f
if spta_img[n_y, n_x]:
n_seg.append([n_y, n_x])
visited[n_y, n_x] = 1
dir = n_dir
cy = n_y
cx = n_x
flag = True
break
if flag == False:
break
segment.append(n_seg)
return segment