해리스 코너 (Harris Corner)
해리스는 모라벡의 마스크를 중심에서 멀어질수록 서서히 값이 작아지는 가우시안 마스크 G(x,y)로 대치하였다.
이렇게 해서 Sum of Squared Difference(SSD)는 다음의 가중치 제곱차의 합(Weighted Sum of Squared Difference(WSSD))로 확장된다.
\[S(v,u) = \sum_{y} \sum_{x} G(y,x)(f(y+v,x+u)-f(y,x))^2\]
위의 식은 특징이 될 가능성을 좀더 정밀하게 측정해 주는데, 실제 구현할 때 몇 가지를 고려해야 한다. 이중 가장 중요한 문제는 (v,u)를 어떻게 변화시켜 주위를 조사할 것인지에 관한 것이다.
모라벡의 경우 한 화소만 이동시켜 동서남북(S(0,1),S(0,-1),S(1,0),S(-1,0))을 조사 했다. 하지만 이러한 경우 모든 방향을 동등하게 취급하는 등방성(isotropic property)를 만족하지 못한다.
해리스는 등방성을 만족하기 위해 미분을 도입했다. 테일러 확장(Taylor expansion)에 따르면 아래의 식이 성립한다.
dx와 dy는 각각 [-1,0,1], [-1,0,1]^T 마스크를 영상에 적용한 영상이다.
\[f(y+v,x+u) \cong f(y,x) + vd_{y}(y,x) + u d_{x}(y,x)\]
이 식을 S(v,u) 식에 대입하면 아래의 식을 얻는다.
\[S(v,u) \cong \sum_{y} \sum_{x} G(y,x)(vd_{y}(y,x)+ud_{x}(y,x))^2\]
해리스는 이 식에서 더 나아가 (v,u)를 바꾸어 가며 인근을 조사하는 것이 아닌, 현재 위치의 영상 ‘구조’를 나타내는 무엇인가를 도출하기 위해 다음과 같이 식을 옮겼다.
\(S(v,u)\)
\(\cong \sum_{y} \sum_{x} G(y,x) (vd_{y}+ud_{x})^2\)
\(=\sum_{y} \sum_{x} G(y,x) (v^2d_{y}^2+2vud_{y}d_{x}+u^2d_{x}^2)\)
\(=\sum_{y} \sum_{x} G(y,x) \begin{pmatrix}v & u \end{pmatrix} \begin{pmatrix}d_{y}^2 &d_{y}d_{x} \\ d_{y}d_{x} & d_{x}^2 \end{pmatrix} \begin{pmatrix} v \\ u\end{pmatrix} \\\)
\(=\begin{pmatrix}v & u \end{pmatrix} \sum_{y} \sum_{x} G(y,x) \begin{pmatrix}d_{y}^2 &d_{y}d_{x} \\ d_{y}d_{x} & d_{x}^2 \end{pmatrix} \begin{pmatrix} v \\ u\end{pmatrix}\)
\(= \begin{pmatrix}v & u \end{pmatrix} \begin{pmatrix}\sum_{y} \sum_{x} G(y,x)d_{y}^2 & \sum_{y} \sum_{x} G(y,x)d_{y}d_{x} \\\sum_{y} \sum_{x} G(y,x)d_{y}d_{x} & \sum_{y} \sum_{x} G(y,x)d_{x}^2 \end{pmatrix} \begin{pmatrix}v \\ u \end{pmatrix}\)
\(= \begin{pmatrix}v & u \end{pmatrix}\begin{pmatrix} G \circledast d_{y}^2 & G \circledast d_{y}d_{x} \\ G \circledast d_{y}d_{x} & G \circledast d_{x}^2 \end{pmatrix} \begin{pmatrix}v \\ u \end{pmatrix}\)
\(= \mathbf{uAu^{T}}\)
여기서 행렬 A는 해리스가 제안한 코너 검출 알고리즘에서 핵심적인 역할을 한다.
행렬 A는 자가 공관계(auto-correlation) 행렬 또는 2차 모멘트 행렬(second moment matrix)이라 불린다.
행렬 A는 (v,u)와 무관하게 계산할 수 있기 때문에 모라벡 알고리즘 처럼 일일히 (v,u)를 옮겨가며 계산할 필요가 없다.
다음과 같이 세점의 2차 모멘트 행렬이 있다고 가정해보자.
| |
a |
b |
c |
| 2차 모멘트 행렬 |
\(A=\begin{pmatrix}0.522 & -0.199 \\ -0.199 & 0.527 \end{pmatrix}\) |
\(A=\begin{pmatrix}0.522 & -0.199 \\ -0.199 & 0.527 \end{pmatrix}\) |
\(A=\begin{pmatrix}0.522 & -0.199 \\ -0.199 & 0.527 \end{pmatrix}\) |
| 고유값 |
\(\lambda_{1}=0.7235, \lambda_{2}=0.3255\) |
\(\lambda_{1}=0.8087, \lambda_{2}=0.0673\) |
\(\lambda_{1}=0.0, \lambda_{2}=0.0\) |
| 특징 가능성 값 |
\(C=0.1925\) |
\(C=0.0237\) |
\(C=0.0\) |
각 행렬의 고유값을 보고 세가지 경우로 나눈다.
- c와 같이 두 개의 고유값 모두 0이거나 0에 가까우면 변화가 거의 없는 픽셀이다.
- b와 같이 고유값 하나는 크고 하나는 작으면 그곳은 한 방향으로만 변화가 있는 에지이다.
- a와 같이 고유값 두 개가 모두 크면 그곳은 여러 방향으로 변화가 있는 지점이다. 이곳이 특징점으로 적합하다.
해리스는 위의 세개의 경우가 일반적으로 적용할 수 있는 규칙임을 입증하고, 이를 바탕으로 고유값 두 개로 정의되는 식을 제안했다.
\[C=\lambda_{1} \lambda_{2} - k(\lambda_{1}+\lambda_{2})^2\]
위 식은 두 고유값이 모두 클 때만 큰 값을 가지므로 특징점일 가능성을 측정하는데 용이하다.
여기서 k는 하이퍼파라미터이다. 보통 0.04 정도가 적절한 것으로 알려져 있다.
하지만 이 식은 계산의 효율면에서 부족하다. 고유값을 계산하는데 약간의 시간이 소요되기 때문이다.
고유값의 성질을 이용해 다음을 적용할 수 있다.
\(\mathbf{A} = \begin{pmatrix}p&r\\r&q \end{pmatrix} 일 때\),
\(\lambda_{1}+\lambda_{2}=p+q=trace(\mathbf{A})\)
\(\lambda_{1} \lambda_{2} = pq-r^2 = det(\mathbf{A})\)
따라서 C는 다음과 같이 쓸 수 있다.
\[C=det(\mathbf{A})-k \times trace(\mathbf{A})^2=(pq-r^2)-k(p+q)^2\]
코드 구현
다음과 같이 0,1로 이루어진 이미지가 있다고 가정하자. 위의 표에서 a,b,c는 각각 이 이미지의 [7,7],[5,3],[2,8]에 해당한다.
import matplotlib.pyplot as plt
from util import *
import numpy as np
import cv2
img = np.zeros([12,12])
img[3:8,3]=1
img[4:8,4]=1
img[5:8,5]=1
img[6:8,6]=1
img[7,7]=1
plt.imshow(img,cmap='gray')
plt.show()
convolution 연산은 지난번에 구현한 im2col을 사용한다. 그리고 가우시안 마스크를 만드는 함수를 새로 작성했다.
def get_gaussian_kernel(sigma,size):
if size % 2 == 0:
size += 1
aran = np.arange(-1 * (size // 2), size // 2 + 1)
XX, YY = np.meshgrid(aran, aran)
ker = gaussian2d(XX, YY, sigma)
ker = ker/np.sum(ker) # normalization
return ker
파이썬의 경우 다음과 같이 하면 [-1,0,1]^T, [-1,0,1] 마스크를 적용한 것과 같다.
mask = get_gaussian_kernel(1, 3)
dy = np.pad(img[1:],((0,1),(0,0))) - np.pad(img[:-1],((1,0),(0,0))) # [-1,0,1]^T 마스크를 적용한 것과 동일
dx = np.pad(img[...,1:],((0,0),(0,1))) - np.pad(img[...,:-1],((0,0),(1,0))) # [-1,0,1] 마스크를 적용한 것과 동일
이제 A행렬의 경우 위의 식과 동일하게 구해진 미분 행렬을 하다마르곱을 한 뒤 가우시안 필터를 적용한다. 이 행렬의 값을 확인하면 위의 표와 일치하는 것을 확인할 수 있다.
>>> A_01 = np.expand_dims(conv(dx * dy, mask), -1)
>>> A_00 = np.expand_dims(conv(dy * dy, mask), -1)
>>> A_11 = np.expand_dims(conv(dx * dx, mask), -1)
>>> A = np.concatenate([np.concatenate([A_00, A_01], -1),
np.concatenate([A_01, A_11], -1)], 2)
>>> print("point a\n",A[7,7])
>>> print("point b\n",A[5,3])
>>> print("point c\n",A[2,8])
point a
[[ 0.52175143 -0.19895501]
[-0.19895501 0.52697637]]
point b
[[ 0.07511361 -0.07511361]
[-0.07511361 0.80104499]]
point c
[[0. 0.]
[0. 0.]]
특징 가능성 C 역시 위 표와 동일하다.
>>> k=0.04
>>> deter = np.linalg.det(A)
>>> trace = np.trace(np.transpose(A, (2, 3, 0, 1)))
>>> C = deter - (k* (trace ** 2))
>>> print("point a\n",C[7,7])
>>> print("point b\n",C[5,3])
>>> print("point c\n",C[2,8])
point a
0.19137437611297517
point b
0.023821169676266046
point c
0.0
이번에는 다음의 사진에서 해리스 코너를 검출해보자.
img = cv2.imread('./data/red_deer.jpg',cv2.IMREAD_GRAYSCALE)
plt.figure(figsize=(14,14))
plt.imshow(img,cmap='gray')
plt.show()

헤리스 코너는 다음과 같이 함수화 하였다. 아래에 use_det 같은 경우는 본문에서 쓴 바와 같이 두 개의 구현이 실제로 시간적인 차이가 있는지 확인하기 위해 구현한 것이다.
방금 삼각형이 그려진 이미지와는 다르게 opencv를 이용해 불러온 이미지는 255의 최대값을 가지므로 normalization을 해주어야 한다.
import time
def Harris_corner(img,threshold,use_det=True,k=0.04,max_value=255):
mask = get_gaussian_kernel(1, 3)
img = img/max_value
dy = np.pad(img[1:],((0,1),(0,0))) - np.pad(img[:-1],((1,0),(0,0)))
dx = np.pad(img[...,1:],((0,0),(0,1))) - np.pad(img[...,:-1],((0,0),(1,0)))
A_01 = np.expand_dims(conv(dx * dy, mask), -1)
A_00 = np.expand_dims(conv(dy * dy, mask), -1)
A_11 = np.expand_dims(conv(dx * dx, mask), -1)
A = np.concatenate([np.concatenate([A_00, A_01], -1), np.concatenate([A_01, A_11], -1)], 2)
if use_det:
deter = np.linalg.det(A)
trace = np.trace(np.transpose(A, (2, 3, 0, 1)))
C = deter - (k* (trace ** 2))
else:
eigens = np.linalg.eigvals(A)
C = eigens[..., 0] * eigens[..., 1] - (k * ((eigens[..., 0] + eigens[..., 1]) ** 2))
return np.where(C>threshold,C,0)
또한 검출된 코너를 시각화 하기 위해 다음과 같은 함수를 작성했다. cv2.circle은 이미지에 원을 그려주는 함수인데 x와 y의 순서에 주의를 해야한다.
def draw_harris_circle(img,harris,print_harris_value=False):
ys, xs = np.where(harris > 0)
gray = np.expand_dims(img, -1)
harris_img = np.concatenate([gray, gray, gray], -1)
for i in range(len(ys)):
harris_img = cv2.circle(harris_img, (xs[i], ys[i]), 10, (0, 0, 255),-1) # (x,y)로 들어감
if print_harris_value:
print("y = {}, x = {}, C = {}".format(ys[i],xs[i],harris[ys[i],xs[i]]))
return harris_img
start=time.time()
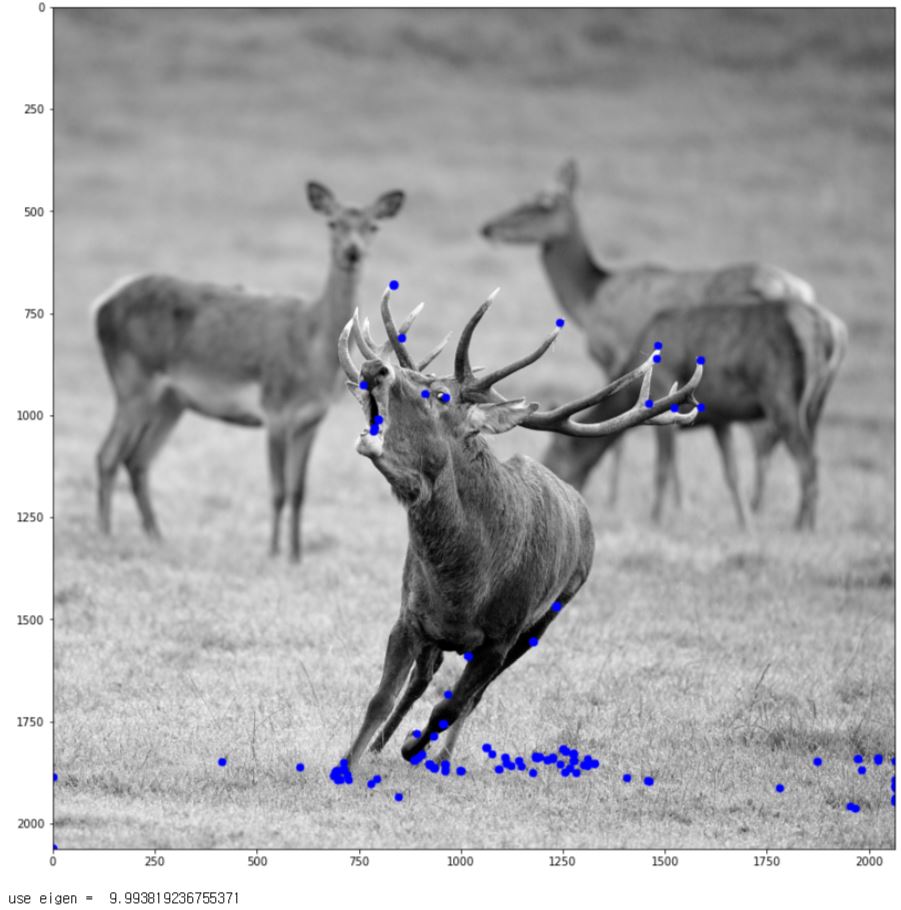
harris = Harris_corner(img,0.02,False)
plt.figure(figsize=(14,14))
plt.imshow(draw_harris_circle(img,harris))
plt.show()
print("use eigen = ", time.time()-start)
start=time.time()
harris = Harris_corner(img,0.02,True)
plt.figure(figsize=(14,14))
plt.imshow(draw_harris_circle(img,harris))
plt.show()
print("use det = ", time.time()-start)
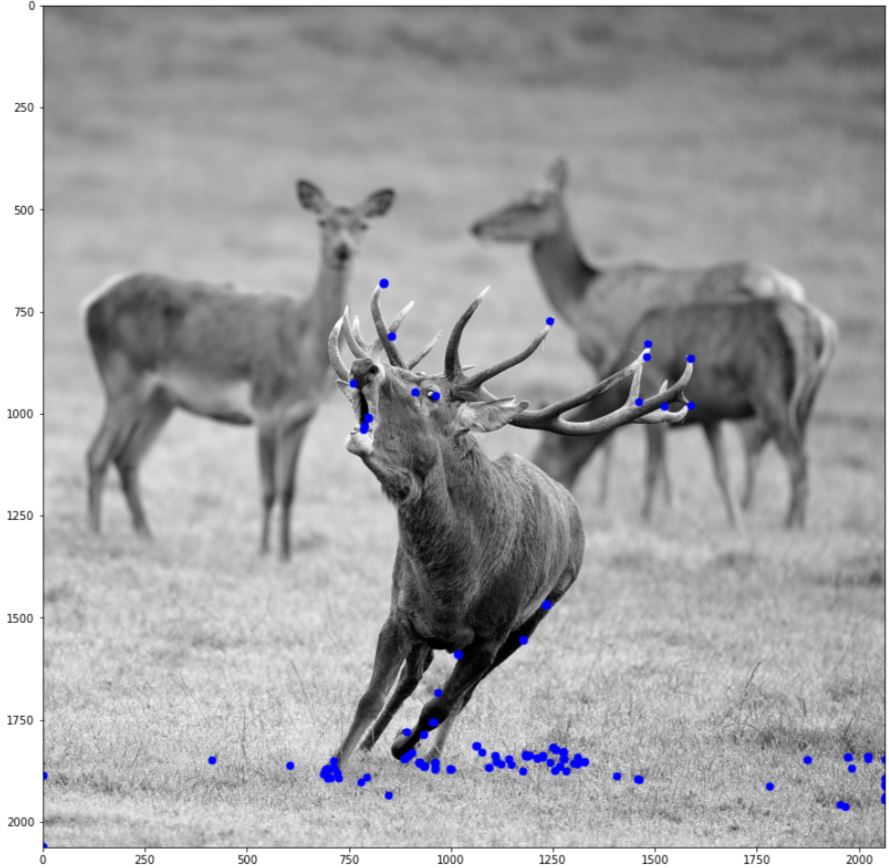
구현에 따라 분명히 차이가 날 것이고 더 좋은 구현이 있을 것이다. 우선은 고유값을 구하는 데에 시간이 오래 걸린다 정도만 기억 하자. 또한, 두 개의 결과가 동일하다는 것도 볼 수 있다.
해리스는 특징점 검출 알고리즘을 코너 검출기(Corner detector)라고 불렀다.하지만 위의 사진에서는 사슴의 뿔 끄트머리 뿐 아니라 눈동자도 검출 되었다. 이러한 이유로 시간이 지나면서 사람들은 코너라는 용어보다 특징점(feature point) 또는 관심점(interest point)을 주로 사용하게 된다.
코드링크
모라벡 알고리즘 (Moravec Algorithm)
-
모라벡 알고리즘은 코너를 검출하는 알고리즘이며 1970년 후반에 발표되었다.
모라벡은 아래의 제곱합의 오차(SSD(Sum of Squared Difference))를 사용해 특징점으로 확률이 높은 픽셀에 대해서는 높은 값을, 특징점으로 확률이 낮은 픽셀에 대해서는 낮은 값을 부여 했다.
\[S(v,u) = \sum_{y} \sum_{x} w(y,x)(f(y+v,x+u)-f(y,x))^2\]
여기서 f(.,.)는 입력 영상이고 w(.,.)는 마스크이다.
마스크는 사이즈를 벗어난 부분에 대해 0으로 취급한다고 생각하면 된다.
예를들어 마스크의 사이즈가 3이고 좌표 (5,3)에 대해 x와 y의 범위는 각각 4~6, 2~4이다.
모라벡에서는 S(0,1),S(0,-1),S(1,0),S(-1,0) 중 최소값을 ‘특징 가능성’값으로 판단한다.
\[C=min(S(0,1),S(0,-1),S(1,0),S(-1,0))\]
코드 구현
import numpy as np
import cv2
import matplotlib.pyplot as plt
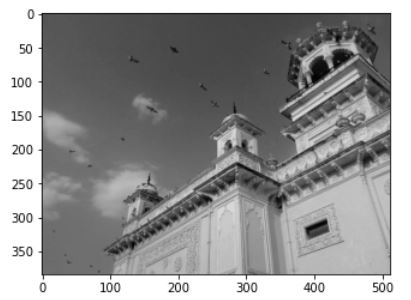
img =cv2.imread('./data/home.jpg',cv2.IMREAD_GRAYSCALE)
plt.imshow(img,cmap='gray')
plt.show()
마스크의 크기는 편의를 위해 3으로 고정했다. 아래와 같이 각각의 방향에 대해 미리 변화량을 계산하고 마스크의 크기만큼 각 좌표에 할당한다. 마지막 confidence는 각 S의 합 중 최소값으로 한다.
def moravec(img):
h,w = img.shape
SSD01 = (img-np.pad(img[...,1:],((0,0),(0,1))))**2
SSD01[...,-1]=0
SSD01 = np.pad(SSD01,((1,1),(1,1)))
SSD0m1 = (img - np.pad(img[..., :-1], ((0, 0), (1, 0)))) ** 2
SSD0m1[..., 0] = 0
SSD0m1 = np.pad(SSD0m1, ((1, 1), (1, 1)))
SSD10 = (img-np.pad(img[1:],((0,1),(0,0))))**2
SSD10[-1,...]=0
SSD10 = np.pad(SSD10, ((1, 1), (1, 1)))
SSDm10 = (img-np.pad(img[:-1],((1,0),(0,0))))**2
SSDm10[0,...]=0
SSDm10 = np.pad(SSDm10, ((1, 1), (1, 1)))
S01=np.zeros([h,w,3,3])
S0m1 = np.zeros([h, w, 3, 3])
S10 = np.zeros([h, w, 3, 3])
Sm10 = np.zeros([h, w, 3, 3])
for i in range(h):
for j in range(w):
S01[i,j]=SSD01[i:i+3,j:j+3]
S0m1[i,j] = SSD0m1[i:i+3,j:j+3]
S10[i,j] = SSD10[i:i+3,j:j+3]
Sm10[i,j] = SSDm10[i:i+3,j:j+3]
confidence = np.min([np.sum(np.sum(S01,axis=2),axis=2),np.sum(np.sum(S0m1,axis=2),axis=2),np.sum(np.sum(S10,axis=2),axis=2),np.sum(np.sum(Sm10,axis=2),axis=2)],axis=0)
return confidence,(S01,S0m1,S10,Sm10)
위의 이미지에서 하늘의 좌표(100,280)와 기둥의 뾰족한 부분(123,283)에 대해(이미지에서 파란점과 붉은점으로 표시했다.) S를 이미지화 하면 다음과 같다.
_,Ss = moravec(img)
img_ex = np.expand_dims(img,-1)
plt.figure(figsize=(15,15))
tmp_img= np.concatenate([img_ex,img_ex,img_ex],-1)
tmp_img[128,283,0]=255
tmp_img[128,283,1]=0
tmp_img[128,283,2]=0
tmp_img[100,280,0]=0
tmp_img[100,280,1]=0
tmp_img[100,280,2]=255
roi = tmp_img[80:140,250:320]
plt.imshow(roi)
plt.show()
fig=plt.figure(figsize=(13,13))
plt.subplot(421)
plt.imshow(Ss[0][129,284],cmap='gray')
plt.xlabel('S01_red')
plt.subplot(423)
plt.imshow(Ss[1][129, 284], cmap='gray')
plt.xlabel('S0m1_red')
plt.subplot(425)
plt.imshow(Ss[2][129, 284], cmap='gray')
plt.xlabel('S10_red')
plt.subplot(427)
plt.imshow(Ss[3][129, 284], cmap='gray')
plt.xlabel('Sm10_red')
plt.subplot(422)
plt.imshow(Ss[0][101, 281], cmap='gray')
plt.xlabel('S01_blue')
plt.subplot(424)
plt.imshow(Ss[1][101, 281], cmap='gray')
plt.xlabel('S0m1_blue')
plt.subplot(426)
plt.imshow(Ss[2][101, 281], cmap='gray')
plt.xlabel('S10_blue')
plt.subplot(428)
plt.imshow(Ss[3][101, 281], cmap='gray')
plt.xlabel('Sm10_blue')
fig.tight_layout()
plt.show()

특징 검출의 역사
대응점 찾기 문제에서는 특징점으로 무엇을 쓸 것인지 결정하는 문제가 중요하다.
에지는 물체의 경계에 위치하지만 그 자체로는 에지 강도와 에지 방향에 대한 정보만 있으므로 매칭에 참여하기에는 부족하다. 특징점은 ㅇㅇ상의 다른 곳과 두드러지게 달라서 풍부한 정보를 추출할 수 있어야 한다.
1970년대에는 에지 화소를 연결하여 얻은 에지 토막에 의지 했다. 기본원리는 에지 토막에서 곡률(Curvature)이 큰 지점을 찾고 그곳을 코너(Corner) 특징으로 취하는 것이다.
이 방법에는 디지털 공간에 정의된 곡선이므로 곡률을 계산하는 데 어려움이 발생하며 작은 물체와 큰 물체 사이의 스케일 변화를 적절히 다루어야 하는 문제가 있다.
에지 토막을 이용하는 연구는 1980년대에 왕성하게 발표 되었다가 2000년 대에는 드물게 나타 난다.
2000년대 부터는 지역 특징(Local featrue)을 이용한 연구결과 위주로 발표된다. 지역 특징은 에지에 의존하는 대신 명암 영상에서 직접 검출한다. 따라서 다른 곳과 두드러지게 다르고 풍부한 정보를 가진 위치를 찾는 정교한 연산자를 설계하는 일이 핵심이다.
이전의 에지 토막 방식은 검출된 코너가 실제 무체의 코너에 해당해야 한다는 가정이 필요했다. 즉 물리적 의미를 중요하게 본 것이다.
이와는 다르게 지역 특징은 반복성을 중요하게 생각한다. 영상 매칭은 한 영상에서 추출된 특징이 다른 영상에서도 추출되면 가능하다는 가정이다.
지역 성질의 특징
지역 특징은 종류에 따라 조금씩 다르지만 일반적으로 위치, 스케일, 방향, 특징 벡터 정보로 구성된다.
검출 단계는 위치와 스케일, 기술 단계는 방향과 특징 벡터를 알아낸다. 이때 검출은 여러 변환에 공변(covariant)이어야 한다. 물체가 이동 또는 회전하거나 스케일이 달라지면 그에 따라 위의 벡터 정보들이 변해야 하기 때문이다. 물체 입장에서 생각해 불변(invariant)라고도 한다.
특징 벡터를 추출하는 기술 단계는 불변(invariant)이어야 한다. 다른 두 사진은 다른 각도나 시간에 의해 명암이 다를 수 밖에 없다. 하지만 본질적인 명암 구조는 같으므로 스케일, 회전, 조명 변화에 무관하게 같은 값을 갖는 특징 벡터를 추출하는 알고리즘을 사옹한다.
지역 특징을 다양한 응용에 활용하기 위해서는 다음의 몇 가지 특성을 만족해야 한다.
- 반복성(repeatability) : 같은 물체를 다른 시점에서 찍은 두 영상이 주어졌을 때, 한 영상 속 물체에서 검출된 특징은 다른 영상의 물체에서도 유사한 위치에 동일한 속성값으로 검출되어야 한다.
- 분별력(distinctiveness) : 물체의 다른 곳과 충분히 구분될 수 있을 정도로 두드러진 속성값을 가져야 한다. 그래야 실제 대응되는 두 점이 유일하게 1:1로 매칭될 수 있다.
- 지역성(locality) : 어떤 점을 중심으로 작은 크기의 주변 영역만 보고 특징 검출과 특징 기술이 수행되어야 한다. 이 특성은 폐색(Occlusion)과 혼재(Clutter)가 발생하는 상황에서 robust하기 위해 필수적이다.
- 정확성(accuracy) : 검출된 특징은 정확한 위치에 놓여야 한다. 스케일 공간에서 찾은 특징은 2차원 공간뿐 아니라 스케일 축에서도 정확해야 한다. 상황에 따라 부분 화소 정확도(subpixel accuracy)까지 계산할 필요가 있다.
- 정당한 양 : 어떤 물체의 pose를 계산하기 위해서는 이론적으로 세 개의 대응점만 있으면 된다. 하지만 대응점에 오류가 포함될 가능성이 있으므로 대응점이 많아지면 보다 정확하게 자세를 추정할 수 있다. 또한 다른 영상에서 대응점이 없을 수도 있다. 따라서 특징은 충분한 양을 얻을 수 있어야 한다. 물론 너무 많은 경우 계산하는데 너무 오랜 시간이 걸리고 매칭의 정답률이 낮아질 수 있다. 그래서 대부분의 특징 검출 알고리즘은 양을 조절하는 매개변수를 포함한다.
- 계산 효율 : 특징 정보를 추출하는 전체 과정을 충분히 빠른 시간 안에 마칠 수 있어야 한다. 검출, 기술, 매칭의 세 단계 중 주로 매칭에 가장 많은 시간을 소요하는데 실시간 처리가 필요한 응용에서는 계산 효율을 늘리는 게 가장 중요하다.
이 특성은 서로 trade-off 관계에 있기 때문에 응용에 따라 적절히 비중을 정해야 한다.
14 Jun 2020
•
TIL
6/08~14
하루에 1개씩 알고리즘 문제를 풀었다. 그래프 관련 문제에 취약한 것 같다. 그리고 시뮬레이션의 문제의 경우 구현에는 문제가 없는데 구현 속도에 문제가 있다.
현재 딥러닝 컴퓨터 비전 완벽 가이드를 섹션 5까지 수강했다.
강의 내용이 정확하게 모델을 어떻게 설계했는지, 어떠한 방식을 사용했는데 이게 어떤원리인지를 설명하는게 아니라 말그대로 코드에 필요한 최소한의 지식을 설명하는 방식이다. 그래서 남은 섹션 3개를 빨리 듣고 이에 대해 공부를 추가적으로 해야 한다.
물론 사용해보지 않았던 google cloud나 처음 알았던 open source 혹은 dataset에 대한 지식을 알려주는 면에서는 긍정적이고 가볍게 object detection의 코드가 어떤식이구나 알기를 원하면 추천한다.
추가적으로 오늘은 ransac 구현 및 정리를 했다.
너무 계획없이 공부량을 늘린면도 없지 않아서 트렐로 이용해서 일정 정리를 좀 해야 겠다.
코드링크
RANSAC(RANdom SAmple Consensus)
RANSAC은 인라이어(inlier)와 아웃라이어(outlier)가 혼합되어 있는 샘플 집합이 주어진 상황에서 인라이어를 찾아 어떤 모델을 적용시키는 일반적인 기법이다. 다만, 무작위로 수를 생성해 인라이어 군집을 찾아내는 과정을 반복해서 임의성을 지닌다.
RANSAC은 에지의 집합에서 직선을 찾아내는 일에 도입해 쓰기도 하는데 이때 에지 화소의 집합이 샘플 집합이 되고, 모델은 직선의 방정식 y=ax+b 에서 a와 b를 예측하는 모델이다.
RANSAC의 원리는 다음과 같다.
-
에지 화소 두 개를 임의로 선택한다.
-
이 두 점으로 직선의 방정식을 계산한다.
\(y=ax+c\) 일 때, 두 점 \((x1,y1)\), \((x2,y2)\)에 대해
\(a = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\
c = y_{1}-ax_{1}\).
- 에지인 화소 중 이 직선과 거리가 허용오차 d 이내인 점을 inlier로 한다.
a’x+b’y+c’=0을 만족하는 직선을 때, 새로운 x_{n}과 y_{n}에 대해 직선과의 거리는
\(distance=\frac{\begin{vmatrix}a'x_{n}+b'y_{n}+c' \end{vmatrix}}{\sqrt{a'^{2}+b'^{2}}}\).
- 1~3을 n번 반복하며 inlier의 개수가 가장 큰 직선을 취한다.
- 이 직선을 최소자승법을 이용해 최적화 한다.
코드 구현
이전에 작성한 util에서 canny함수를 사용해 영상을 이진화 한다.
import cv2
import numpy as np
import matplotlib.pyplot as plt
from util import *
img = cv2.imread('./data/pic6.png')
fig = plt.figure(figsize=(13,13))
plt.subplot(121)
plt.imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB))
canny_img = canny(cv2.cvtColor(img,cv2.COLOR_BGR2GRAY),30,70)
plt.subplot(122)
plt.imshow(canny_img,cmap='gray')
fig.tight_layout()
plt.show()
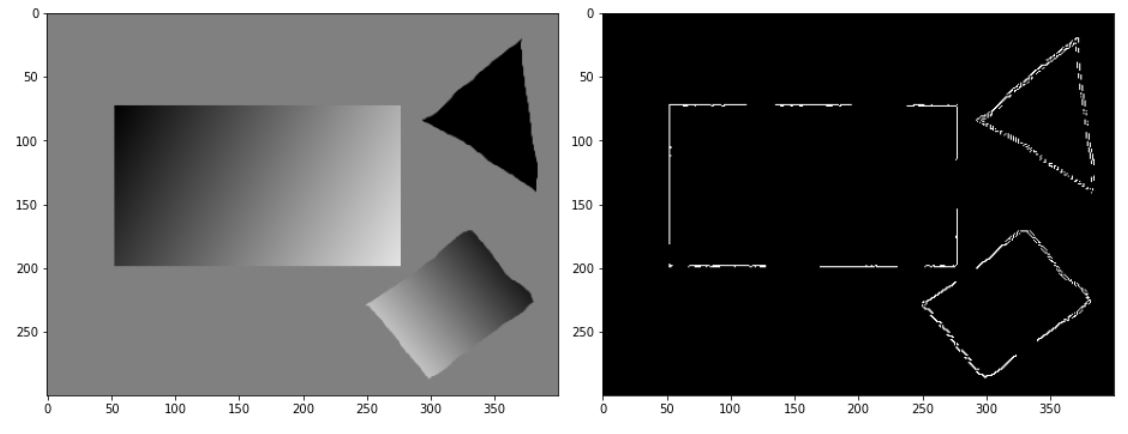
먼저 edge인 픽셀에 대해 랜덤으로 2개의 점을 선택하고 이를 이용해 직선의 방정식을 도출해야한다.
직선의 거리를 계산하기 위해 먼저 ax+by+c = 0 식을 만족 하는 (a,b,c)를 return 하도록 함수를 작성했다.
여기서 b는 1로 고정시켰다.
def make_line(y_idxs,x_idxs):
x1,x2,y1,y2=(0,0,0,0)
while x1 ==x2 or y1 ==y2:
ch_idxs = np.random.choice(len(y_idxs), 2, replace=False)
y1 = y_idxs[ch_idxs[0]]
x1 = x_idxs[ch_idxs[0]]
y2 = y_idxs[ch_idxs[1]]
x2 = x_idxs[ch_idxs[1]]
slope = (y2-y1) /(x2-x1)
c = -(y1-(x1*slope))
return (-1*slope,1,c) # ax+by+c=0
>>> y_idxs,x_idxs= np.where(canny_img) # canny_img에서 True인 배열의 인덱스를 반환한다.
>>> m_slope,one,m_bias = make_line(y_idxs,x_idxs)
>>> print(m_slope,one,m_bias)
0.08256880733944955 1 -208.1559633027523
다음으로 점과 직선의 거리를 구하는 수식을 이용한다. for문을 이용하기 보다 numpy의 함수를 이용하는 방식이 빠르므로 numpy 함수를 이용해 구현했다.
def cal_distance(a,b,c,xx,yy):
return abs(a*xx+b*yy+c)/np.sqrt(a**2+b**2)
x_range = np.arange(canny_img.shape[1])
y_range = np.arange(canny_img.shape[0])
xx,yy = np.meshgrid(x_range,y_range)
>>> cal_distance(m_slope,one,m_bias,xx,yy)
array([[207.45000808, 207.3677193 , 207.28543052, ..., 174.78136341,
174.69907463, 174.61678586],
[206.45339955, 206.37111077, 206.288822 , ..., 173.78475488,
173.70246611, 173.62017733],
[205.45679102, 205.37450225, 205.29221347, ..., 172.78814636,
172.70585758, 172.6235688 ],
...,
[ 88.54272459, 88.62501337, 88.70730215, ..., 121.21136926,
121.29365804, 121.37594681],
[ 89.53933312, 89.6216219 , 89.70391067, ..., 122.20797779,
122.29026656, 122.37255534],
[ 90.53594165, 90.61823042, 90.7005192 , ..., 123.20458631,
123.28687509, 123.36916387]])
지정한 d이내의 오차를 갖으며 edge인 픽셀에 대해 idxs의 목록을 받으려면 다음과 같이 작성하면 된다.
d = 2
idxs = np.where(np.logical_and(cal_distance(m_slope,one,m_bias,xx,yy)<d,canny_img))
>>> idxs
(array([179, 179, 180, 180, 180, 180, 181, 181, 182, 182, 182, 182, 182,
183, 183, 184, 184, 184, 185, 186, 187, 198, 198, 198, 198, 198,
198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198, 198,
198, 198, 198, 198, 198, 198, 198, 198, 198, 199, 199, 199, 199,
199, 199, 199, 199, 199, 199, 199, 199, 199, 199], dtype=int64),
array([338, 341, 317, 339, 341, 342, 315, 316, 312, 313, 314, 315, 341,
311, 312, 277, 310, 311, 277, 277, 277, 99, 100, 101, 102, 103,
104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 117, 118,
119, 120, 121, 122, 123, 124, 125, 126, 127, 87, 88, 89, 90,
91, 103, 115, 116, 119, 123, 124, 125, 126, 127], dtype=int64))
마지막으로 최소 자승법을 이용해 최적의 직선을 찾고 ax+y+c=0을 만족하기 위해 -1을 곱한 결과를 return 하는 함수를 작성한다.
def Least_square(idxs):
'''
:param idxs: (y_idxs,x_idxs)
:return: [a,b]^T = (A^T A)^-1 A^T B where, ax+b=y and A=((x1,1),(x2,1),(x3,1),...), B=((y1),(y2),...)
'''
y_idxs,x_idxs = idxs
x_idxs = np.expand_dims(x_idxs,-1) # (len,1)
y_idxs = np.expand_dims(y_idxs,-1) # (len,1)
A = np.concatenate([x_idxs,np.ones_like(x_idxs)],-1) # (len,2)
slope,bias = np.matmul(np.matmul(np.linalg.inv(np.matmul(A.transpose(),A)),A.transpose()),y_idxs)
return slope*-1,bias*-1
>>> Least_square(idxs)
array([0.07913282]), array([-207.12125678])
ransac의 전체적인 함수는 다음과 같이 작성했다. 주석을 참고하면 된다.
# ax+y+c<1를 만족하는 직선을 이미지내에 그린다.완벽하게 0을 만족하지 않는 경우도 있기 때문에 1로 설정했다.
def draw_line(m_slope,m_bias,xx,yy):
return np.where(abs(xx*m_slope+yy+m_bias)<1,255,0)
def ransac(img,n=50,d=2,return_image=True):
'''
:param img: binary(recommand)
:param n: number of iteration
:param d: tolerance
:param return_image:
True: you can get a straight line image
False: you can get Linear equation
:return:
'''
if len(img.shape)==2:
h,w=img.shape
else:
h,w,c=img.shape
y_idxs,x_idxs= np.where(img)
x_range = np.arange(w)
y_range = np.arange(h)
xx, yy = np.meshgrid(x_range, y_range)
max_line=[0,0,0,0]
# search model
for i in range(n):
m_slope,one,m_bias = make_line(y_idxs,x_idxs)
temp_idxs = np.where(np.logical_and(cal_distance(m_slope,one,m_bias,xx,yy)<d,img))
if len(temp_idxs[0])<2: # 2개 이상이어야 직선의 방정식을 세울 수 있다.
continue
if max_line[0]<len(temp_idxs[0]): # 현재 찾은 직선보다 더 많은 점들을 포함하는 경우 교체한다.
max_line = [len(temp_idxs[0]),m_slope,m_bias,temp_idxs]
# optimization line
optimal_param = Least_square(max_line[-1])
if return_image:
original_line = draw_line(max_line[1],max_line[2],xx,yy)
optimal_line = draw_line(optimal_param[0],optimal_param[1],xx,yy)
return original_line,optimal_line
else:
optimal_line = [max_line[0],optimal_param[0],optimal_param[1],max_line[3]]
return max_line,optimal_line
직선의 이미지를 원본에 그리기 위해서 다음과 같은 함수를 추가로 작성했다.
def draw_line_in_image(line,img):
if len(img.shape) is not 2:
print("Shape of input image must have 2, but this input image have shape of {}".format(len(img.shape)))
return None
r = np.expand_dims(np.clip(line+img,0,255),-1)
g = np.expand_dims(np.where(line,0,img),-1)
b = g
ret = np.concatenate([r,g,b],-1)
plt.imshow(ret)
ransac은 랜덤으로 선택하는 부분 때문에 n이 작으면 작을 수록 실행때마다 다른 값이 나올 확률이 높아진다. 다음의 결과는 최적화가 되기전과 최적화가 된 직선, n이 50인 경우와 5인 경우에 대한 결과이다
fig = plt.figure(figsize=(13,13))
ori_line,optimal_line = ransac(canny_img)
plt.subplot(221)
plt.xlabel('Original line n=50')
draw_line_in_image(ori_line,canny_img)
plt.subplot(222)
plt.xlabel('Optimal line n=50')
draw_line_in_image(optimal_line,canny_img)
ori_line,optimal_line = ransac(canny_img,n=5)
plt.subplot(223)
plt.xlabel('Original line n=5')
draw_line_in_image(ori_line,canny_img)
plt.subplot(224)
plt.xlabel('Optimal line n=5')
draw_line_in_image(optimal_line,canny_img)
plt.show()
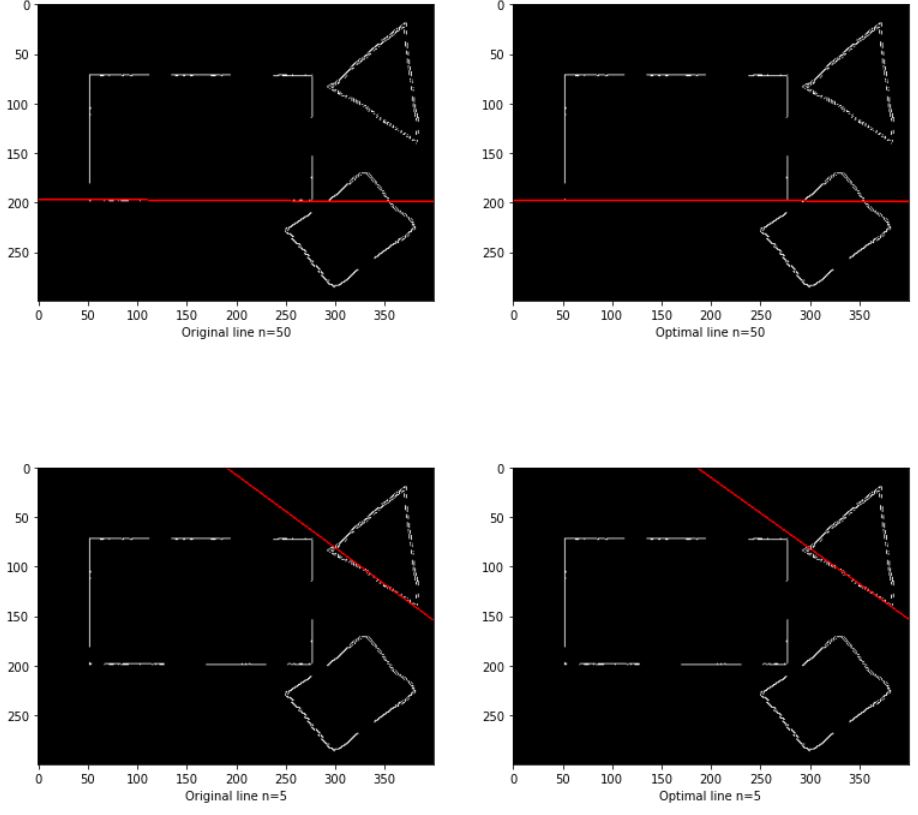
아래의 경우 최적화 전과 후가 잘 차이가 나지 않지만 위의 결과의 경우 좀더 많은 직선을 포함하도록 최적화된 것을 볼 수 있다.







