기대값(Expected value)

기대값

\(X(\omega)\)에 대해 전체 면적을 1로 두고 다음과 같이 표현해보자.

X를 높이로 두면 다음과 같이 3차원으로 표현된다.

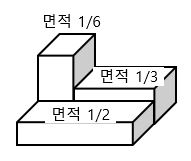
기대값은 평균적으로 기대하는 값을 뜻한다. 이 값은 위 그림의 부피와 같다고 생각하면 된다. \(기대값 E \left[X \right]= (높이 1) \times (바닥 면적 \frac{1}{2}) + (높이2) \times (바닥면적 \frac{1}{3}) +(높이 5) \times (바닥면적 \frac{1}{6}) \\ = 1 \cdot P(X=1)+2 \cdot P(X=2) + 5 \cdot P(X=5) =2\)

기대값의 성질

기대값은 다음과 같은 성질을 가진다.

• \(E[X]=\sum_{k} kP(X=k)\).
• \(E[g(X)]=\sum_{k} g(k)P(X=k)\).

이를 해석하면 다음과 같다.

’\(\Omega\) 위의 각 점 \(\omega\)에 대해 \(g(X(\omega))\)를 높이 축에 찍어서 그래프를 그리며, 그렇게 만들어진 오브제(object)의 부피가 기대값 \(E[g(x)]\) 이다.’