표준 정규 분포
정규분포 혹은 가우스 분포는 다음의 이유로 많이 사용된다.
- 여러 가지 계산이 쉽다.
- 결과 수식이 깔끔하다.
- 현실에서 정규분포로 근사할 수 있는 대상이 많다.
표준 정규분포는 정규분포의 가장 대표적인 형태이며 아래의 식으로 표현되고 평균이 0이고 분산이 1인 정규분포를 뜻한다.
\[f(z) = \frac{1}{\sqrt{2 \pi}} exp \left( -\frac{z^2}{2}\right)\]먼저 exp 안의 2를 임의의 상수로 두고 z에 대해 생각을 해보자. 우리는 다음과 같은 사실을 알 수 있다.
- z의 제곱이므로 좌우 대칭이다.
- z= 0 일 때 0이 된다.
- z가 음의 무한대 혹은 양의 무한대 일 때 음의 무한대로 수렴한다.
다시 exp와 함쳐서 생각하면 다음을 알 수 있다.
- 좌우 대칭이다.
- z=0 일 때 exp값은 최댓값이 된다.
- z가 0에서 멀어질수록 점점 0에 수렴한다.
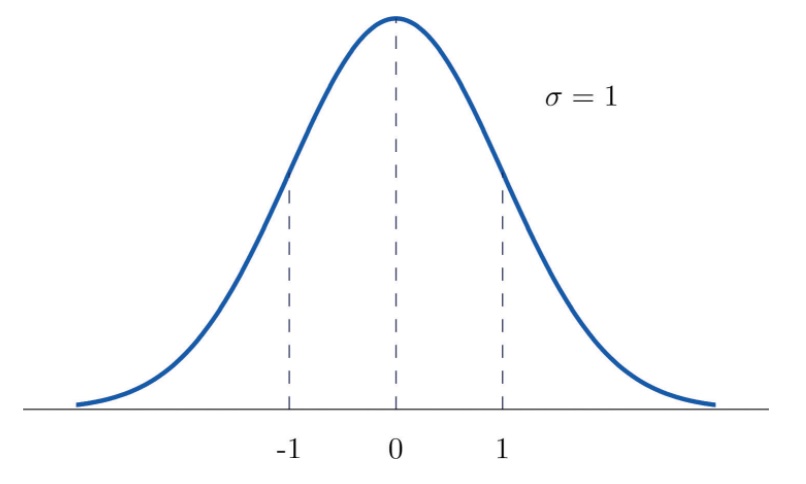
그렇다면 이제 위의 그림을 이해할 수 있다.
상수항에 대한 궁금증은 다음과 같이 해결할 수 있다.
가우스 적분에 의해
\[\int^{\infty}_{-\infty} exp \left( -\frac{z^2}{2}\right)dz = \sqrt{2\pi}\]이 성립하므로 확률에 맞춰 적분이 1이 되도록 하기 위해 \(1/(\sqrt{2\pi})\)가 등장했다.
exp에 포함된 분모 2는 분산을 1로 맞추기 위해 설정된 값이다. 참고로 분산의 식은 아래와 같다.
\[V\left[ Z\right] = \int^{\infty}_{-\infty} z^{2} \frac{1}{\sqrt{2\pi}}exp \left( -\frac{z^2}{2}\right) dz\]일반 정규 분포
일반정규분포는 표준정규분포를 이동하거나 신축한 정규분포라고 생각 할 수 있다.
- \(\mu\) 이동 : \(Y \equiv Z + \mu\)
- \(\sigma\)배 신축 : \(W \equiv \sigma Z \ \ where, \sigma > 0\)
이를 그림으로 표현하면 아래와 같다.
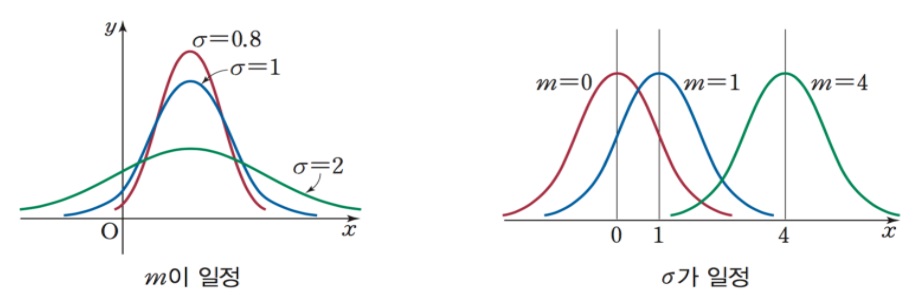
이를 일반적인 식으로 표현하면 아래와 같다.
\[f_{X}(x) = \frac{1}{\sqrt{2 \pi \sigma^2}}exp \left( -\frac{(x-\mu)^2}{2 \sigma^2}\right)\]이렇게 구구절절하게 식으로 표현을 하는 경우는 거의 없고 다음과 같이 정규분포를 표현한다.
\[X \sim N(\mu, \sigma^2)\]여기서 \(\mu\)는 평균, \(\sigma\)는 표준편차를 뜻한다. 처음에 설명했던 표준정규분포는 \(X \sim N(0,1)\)로 표현할 수 있다.
정규 분포 예제
ex1.
Q. 표준정규분포인 \(Z\)에 대해 \(X= \sigma Z+\mu\)이 성립할 때, \(X\) 의 기대값과 분산은?
A.
일반정규분포 구하라는 거다.
\[E \left[ X\right] = E \left[ \sigma Z + \mu \right] = \sigma E \left[ Z \right]+\mu = \mu \\ V \left[ X \right] = V \left[ \sigma Z + \mu \right] = \sigma^{2}V \left[ Z \right] = \sigma^2\]ex2.
Q. 표준정규분포를 \(\mu\)만큼 이동하고 \(\sigma\) 배 했을 때 \(N(\mu, \sigma^2)\) 꼴로 나타낸다면?
A.
\[\sigma \left( Z + \mu\right) = \sigma Z + \sigma \mu \sim N \left( \sigma \mu , \sigma^2 \right)\]ex3.
Q. \(X_{1},X_{2},X_{3},X_{4},X_{5}\)가 독립이고, 모두 정규분포 \(N \left( \mu , \sigma^2 \right)\)를 따른다고 할 때, \(Y \equiv \left( X_{1}+X_{2}+X_{3}+X_{4}+X_{5}\right) / 5\)를 \(N(\mu, \sigma^2)\) 꼴로 나타낸다면?
A.
\[E \left[ Y\right] = E \left[ \frac{X_{1}+X_{2}+X_{3}+X_{4}+X_{5}}{5}\right] = \\ \frac{E\left[X_{1}\right]+E\left[X_{2}\right]+E\left[X_{3}\right]+E\left[X_{4}\right]+E\left[X_{5}\right]}{5} = \frac{\mu+\mu+\mu+\mu+\mu}{5}=\mu \\ V \left[ Y\right] = V \left[ \frac{X_{1}+X_{2}+X_{3}+X_{4}+X_{5}}{5}\right] = \\ \frac{V\left[X_{1}\right]+V\left[X_{2}\right]+V\left[X_{3}\right]+V\left[X_{4}\right]+V\left[X_{5}\right]}{5^2} = \frac{\sigma^2+\sigma^2+\sigma^2+\sigma^2+\sigma^2}{5} = \frac{\sigma^2}{5} \\ \therefore Y \sim N(\mu,\sigma^2 / 5)\]ex4.
Q. \(X \sim N(\mu, \sigma^2)\)에 대해 \(X\)가 \(\mu \pm k \sigma\)의 범주에 드는 확률
A.
\[P(\mu -2\sigma) \le X \le \mu + 2\sigma \approx 0.954 \\ P(\mu -3\sigma) \le X \le \mu + 3\sigma \approx 0.997\]사실 이 값은 계산보다는 참고에 가깝다. 위의 값들은 유명하므로 두개 정도만 알고 있고 나머지 값은 그때그때 찾아보길 권한다.
Comments