확률 0
다음과 같은 확률변수 X를 생각하자
- \(\omega = (u,v) , \ 0 \le u \le 1 , \ 0 \le v \le 1\).
- \(X(\omega)=10u\).
이 경우 \(P(4 \le X \le 7)\) 확률은 아래 그림과 같이 사각형의 면적을 구하면 될 것이다.
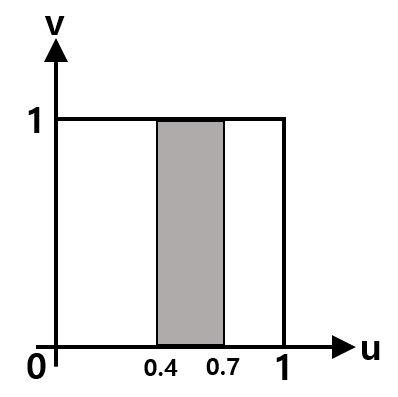
하지만 만약 \(P(X=2)\) 확률을 구하고자 한다면 다음과 같이 구해야 한다.
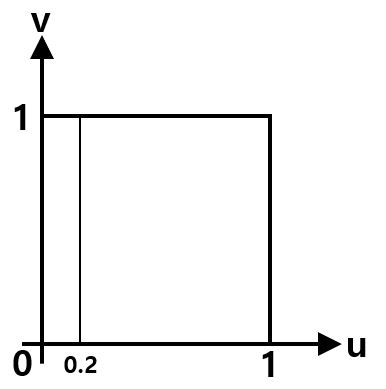
그러면 이 경우에는 \(P(X=2)=0\)이라는 결과가 얻어진다.
이 예제로 연속된 실수값에서는 특정한 확률의 값은 0이 된다는 것을 알 수 있다.
확률 밀도 함수
연속된 실수값에서 확률을 구하기 위해서는 누적분포함수와 확률밀도함수를 사용한다.
여기서 누적분포함수는 ‘X이하의 값이 나올 확률’ 정도로 기억하면 편하다.
확률밀도함수는 말 그대로 확률의 농도라고 해석할 수 있다. 즉, 확률밀도함수의 값이 크다는 것은 그 부근의 확률이 높다는 것을 의미한다. 식은 아래와 같이 누적분포함수의 변화량으로 구할 수 있다.
\[f_{X}(x) \equiv F'_{X}(x)= \frac{dF_{X}(x)}{dx}\]위에서 말한것과 같이 연속값의 확률변수의 순간적인 확률은 정의되지 않는다. 확률변수의 특정한 범위에 대해 그 범위가 나올 확률은 다음과 같이 정의된다.
\[\int_{\beta}^{\alpha}f_{X}(x)dx\]물론 확률의 총합은 1이기 때문에 다음이 성립한다.
\[\int_{-\infty}^{\infty}f_{X}(x)dx=1\]균등 분포
확률밀도함수로 나타내는 확률분포가 구간 \([\alpha,\beta]\) 위의 균등분포일때 식은 다음과 같이 정의된다.
\[f_{X}(x)= \begin{cases} \frac{1}{\beta - \alpha} \ (\alpha \le x \le \beta) \\ 0 \ (기타) \end{cases}\]확률밀도함수의 변수 변환
\(X\)의 확률밀도함수 \(f_{X}\)가 주어져 있을 때, \(Y=3X-5\)라고 할 때 \(Y\)의 확률밀도함수 \(f_{Y}\)를 구해보자.
단순히 생각했을 때는 \(f_{Y}(4) = f_{X}(3)\)이 될 것 같지만 두 확률밀도함수는 서로 선형관계에 있지않다. 자세히 생각해보면 만약 \(f_{X}\)가 범위 \(0 \le X \le 3\)에서 1의 확률을 가진다면 Y는 \(-5 \le Y \le 4\)에서 확률이 1이 될것이다. 오히려 범위가 3배나 증가했고 변화량은 이에 분명히 반비례할 것이다. 변화량이 반비례 하다는 것은 결국 확률밀도 함수는 다음과같이 정의 된다는 것이다.
Comments