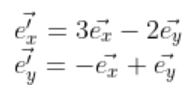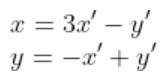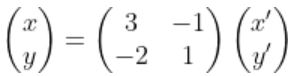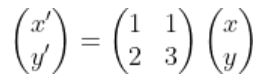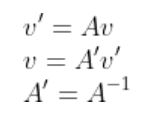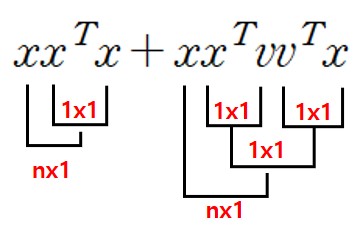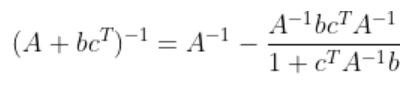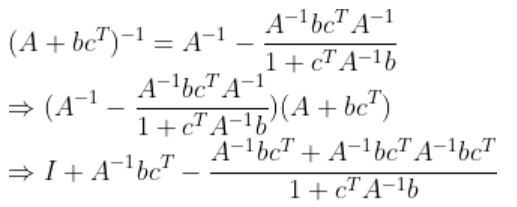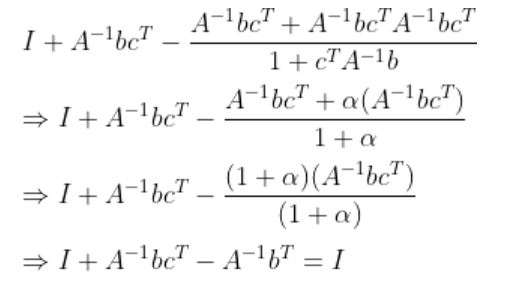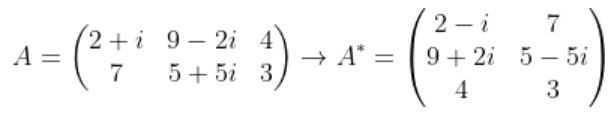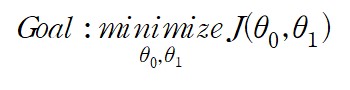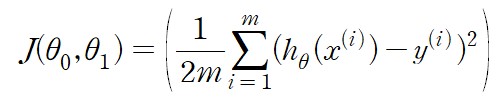02 May 2020
•
Linear Algebra
Transformation and Matrix
-
좌표 변환은 ‘정방행렬 A를 곱한다’라는 형태로 쓸 수 있다. 단, A에는 역행렬이 존재한다.
-
역행렬을 지니는 정방행렬 A를 곱하는 것은 ‘좌표 변환’이라고 해석할 수 있다.
ex)
다음과 같이 2쌍의 기저(e,e’)를 사용해 벡터 v를 다음 두 가지로 표현이 가능한 경우
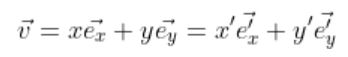
v와 v’의 관계를 나타내보자.
우선 이때 e와 e’의 대응관계가 다음과 같을 경우.
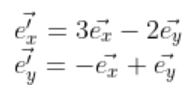
다음과 같이 쓸 수 있다.
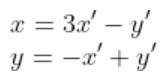
이를 행렬 형태로 나타내면
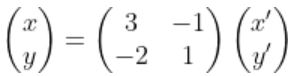
혹은
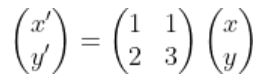
로 쓸 수 있다.
또한, 다음이 성립한다.
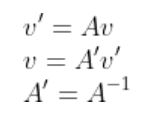
02 May 2020
•
Linear Algebra
Importance of Shape
행렬 계산을 할 때 크기에 주목을 해야 한다!!
아래의 예시를 보며 맘에 새기자
ex1)
Q.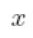 와
와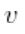 는 각각 n차원의 열 벡터(혹은 종 벡터)일 때,
는 각각 n차원의 열 벡터(혹은 종 벡터)일 때, 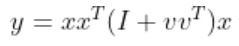 를 계산해라.
를 계산해라.
A.
일반적으로 계산하게 되면 shape은 (nxn)(nxn +(nxn))(nx1)으로 nxn이 많아지게 된다.
하지만 shape에 집중하게 되면 아래와 같이 가능하다.
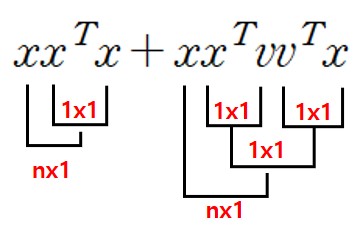
ex2)
Q. A는 n차 정방행렬, b와 c는 n차 열 벡터(혹은 종 벡터) 일 때, 다음이 성립함을 증명해라.
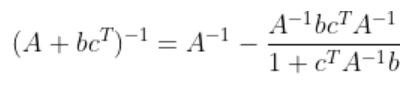
A.
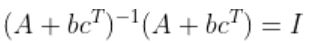 이 성립해야 하므로
이 성립해야 하므로
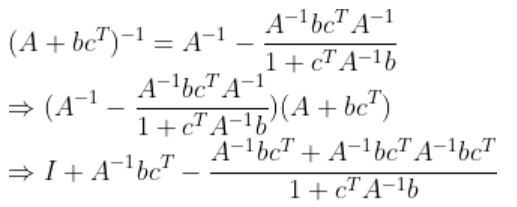
여기서 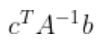 는 Scalar이므로
는 Scalar이므로 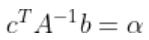 로 두면 식은 다음과 같이 된다.
로 두면 식은 다음과 같이 된다.
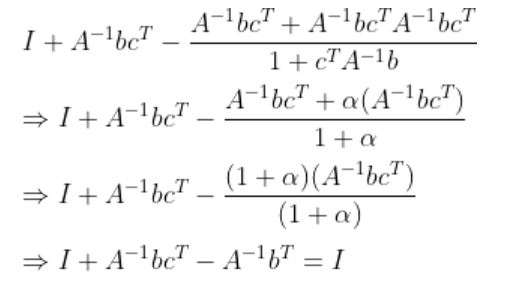
02 May 2020
•
Linear Algebra
conjugate Transpose Matrix
표기법
성질
ex)
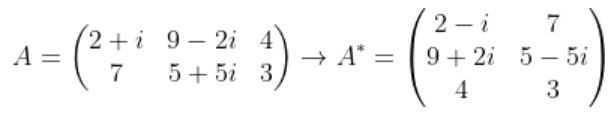
01 May 2020
•
Andrew
list로 가기
Linear regression with one variable
-
용어
-
Supervised learning (감독 학습) : 자료의 정확한 답이 주어진 학습
-
Unsupervised learning (비 감독 학습) : 자료의 정확히 주어지지 않는 학습 (형태에 따라 다양함)
-
Regression (회귀) : 실수 값을 갖는 출력을 예측하는 문제 (분류와 함께 신경망의 대표적인 문제)
-
Classification (분류) : 이산 값(Discrete-value)으로 분류되는 문제
-
Univariate linear regression (단 변량 선형 회귀) : 변수가 하나인 선형 회귀
신경망을 이해하기 위해 다음과 같이 1차 함수 형태로 나타 낼 수 있다.

Cost function ~ Cost function institution
신경망의 목적은 오차가 최소가 되는 파라미터를 찾는 것이다. 오차를 J 라고 했을 때 이 신경망의 최종 목적은 다음과 같다.
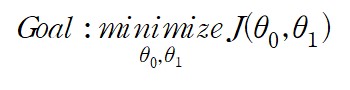
함수 J의 결과값이 가장 작은 theta 0, theta1을 찾는 것이다. 오차 J를 Cost function 혹은 Loss function이라고 한다. 강의에는 J로 표기하지만 논문에 따라 다르며 가장 많이 보이는 것은 Loss의 L을 따온 표기이다.
비용 함수의 방법은 실제로 다양하며 영상에서는 가장 쉽게 사용이 가능한 Mean squared error function에 대해 소개했다. 식은 다음과 같다.
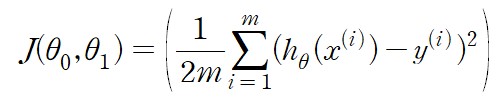
영상에 나온 theta 값들에 따른 J 값이다. 하지만 Mean squared error를 사용했을 때는 theta0 의 영향이 너무 작아 쌍곡선 형태를 볼 수 없다.
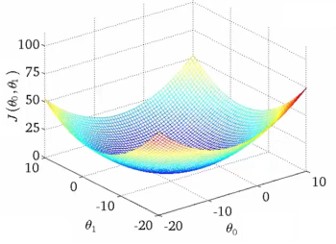
영상에서는 포틀랜드의 집 가격이라는 데이터 셋이 있는지 잘 모르겠다. 찾아봤지만 부동산 내용이 많아 유명한 Boston 집가격 데이터 셋으로 실험을 했다. 식은 위에 나온 수식들을 이용했다.
![]()