Transformation and Matrix
-
좌표 변환은 ‘정방행렬 A를 곱한다’라는 형태로 쓸 수 있다. 단, A에는 역행렬이 존재한다.
-
역행렬을 지니는 정방행렬 A를 곱하는 것은 ‘좌표 변환’이라고 해석할 수 있다.
ex)
다음과 같이 2쌍의 기저(e,e’)를 사용해 벡터 v를 다음 두 가지로 표현이 가능한 경우
![]()
v와 v’의 관계를 나타내보자.
우선 이때 e와 e’의 대응관계가 다음과 같을 경우.
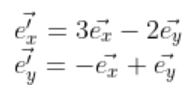
다음과 같이 쓸 수 있다.
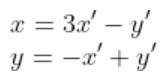
이를 행렬 형태로 나타내면
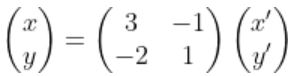
혹은
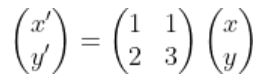
로 쓸 수 있다.
또한, 다음이 성립한다.
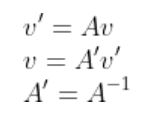
Comments