Monch

가우스 요르단 소거법

가우스 소거법과 가우스 요르단 소거법

다음 세 가지의 기본 행 연산을 통해 연립일차방정식의 첨가행렬(계수행렬과 상수행렬을 묶은 행렬)을 기약 행 사다리꼴로 변환하여 해를 구한다.

1) 한 행을 상수배 한다.

2) 한 행을 상수배하여 다른 행에 더한다.

3) 두 행을 맞바꾼다.

먼저 가우스 소거법부터 살펴보자.

연립 방정식

다음과 같은 연립방정식을 생각해 보자 \(2x_1+3x_2+3x_3=9\\3x_1+4x_2+2x_3=9\\-2x_1-2x_2+3x_3=2\) 이는 2개의 행렬로 나타내면 다음과 같이 나타낼 수 있다. \(A=\begin{pmatrix}2&3&3\\3&4&2\\-2&-2&3\end{pmatrix}, \quad y=\begin{pmatrix}9\\9\\2\end{pmatrix}\) 가우스 소거법에서는 위의 행렬을 하나의 블록 행렬로 나타낸다. \(\left( \begin{array}{ccc|c} 2 & 3 & 3 & 9 \\ 3&4&2&9 \\ -2&-2&3&2 \end{array} \right)\left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\) 여기서 각 행의원소의 앞부분을 소거한다. 과정을 나타내면 다음과 같다. \(\left( \begin{array}{ccc|c} (1) & \frac{3}{2} & \frac{3}{2} & \frac{9}{2} \\ 3 & 4 & 2 & 9 \\ -2&-2&3&2 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \Rightarrow \left( \begin{array}{ccc|c} 1 & \frac{3}{2} & \frac{3}{2} & \frac{9}{2} \\ (0) & -\frac{1}{2} & -\frac{5}{2} & -\frac{9}{2} \\ (0)&1&6&11 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \Rightarrow \left( \begin{array}{ccc|c} 1 & \frac{3}{2} & \frac{3}{2} & \frac{9}{2} \\ 0 & (1) & 5& 9 \\ 0&1&6&11 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \Rightarrow \left( \begin{array}{ccc|c} 1 & \frac{3}{2} & \frac{3}{2} & \frac{9}{2} \\ 0 & 1 & 5& 9 \\ 0&(0)&1&2 \end{array} \right)\left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\\) 여기까지의 과정을 가우스 소거법이라고 한다. 가우스 요르단(Gauss jordan) 소거법은 여기서 한단계 더 나아간다. \(\left( \begin{array}{ccc|c} 1 & \frac{3}{2} & \frac{3}{2} & \frac{9}{2} \\ 0 & 1 & 5& 9 \\ 0&(0)&1&2 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \Rightarrow \left( \begin{array}{ccc|c} 1 & \frac{3}{2} & \frac{3}{2} & \frac{9}{2} \\ 0 & 1 & (0)& -1 \\ 0&0&1&2 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \Rightarrow \left( \begin{array}{ccc|c} 1 & (0) & \frac{3}{2} & 6 \\ 0 & 1 & 0& -1 \\ 0&0&1&2 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \Rightarrow \left( \begin{array}{ccc|c} 1 & 0 & (0) & 3 \\ 0 & 1 & 0& -1 \\ 0&0&1&2 \end{array} \right) \left(\begin{array}{}x_1\\x_2\\ x_3 \\\hline 1 \end{array}\right)=\begin{pmatrix}0\\0\\0\end{pmatrix}\\\) 이렇게 각 행이 바로 각 \(x_{i}\)의 해를 나타낸다.

역행렬

행렬 \(A\)의 역행렬 \(A^{-1}\)에 대한 관계를 다음과 같이 나타내자 \(A^{-1}(A|I)=(I|A^{-1})\) 이 식을 해석하면 가우스 소거법으로 A를 I로 만들면 우측에는 A의 역행렬이 나타낸다로 이해할 수 있다.

자세한 계산은 다음과 같이 계산된다 \((A|I)\\ \Rightarrow \left( \begin{array}{ccc|ccc} 2 & 3 & 3 & 1 & 0 & 0 \\ \hline 3 & 4 & 2 & 0 & 1 & 0\\ \hline -2 & -2 & 3 & 0 & 0 & 1 \end{array} \right)\\ \Rightarrow \left( \begin{array}{ccc|ccc} (1) & \frac{3}{2} & \frac{3}{2} & \frac{1}{2} & 0 & 0 \\ \hline 3 & 4 & 2 & 0 & 1 & 0\\ \hline -2 & -2 & 3 & 0 & 0 & 1 \end{array} \right)\\ \Rightarrow \left( \begin{array}{ccc|ccc} 1 & \frac{3}{2} & \frac{3}{2} & \frac{1}{2} & 0 & 0 \\ \hline (0) & -\frac{1}{2} & -\frac{5}{2} & -\frac{3}{2} & 1 & 0\\ \hline (0) & 1 & 6 & 1 & 0 & 1 \end{array} \right)\\ \Rightarrow \left( \begin{array}{ccc|ccc} 1 & \frac{3}{2} & \frac{3}{2} & \frac{1}{2} & 0 & 0 \\ \hline 0 & (1) & 5 & 3 & -2 & 0\\ \hline 0 & 1 & 6 & 1 & 0 & 1 \end{array} \right)\\ \Rightarrow \left( \begin{array}{ccc|ccc} 1 & (0) & -6 & -4 & 3 & 0 \\ \hline 0 & 1 & 5 & 3 & -2 & 0\\ \hline 0 & (0) & 1 & -2 & 2 & 1 \end{array} \right)\\ \Rightarrow \left( \begin{array}{ccc|ccc} 1 & 0 & (0) & -16 & 15 & 6 \\ \hline 0 & 1 & (0) & 13 & -12 & -5\\ \hline 0 & 0 & 1 & -2 & 2 & 1 \end{array} \right)\\ =(I|A^{-1})\) 이렇게 바로 \(A\)의 역행렬을 구할 수 있다.

물론 라이브러리에 구현이 되어 있어 손으로 계산할 일이 없지만 손 계산이 필요할 때 기억해 두면 좋을 것 같다.

20/05/04

원래 깃허브 마크다운으로는 latex 문법이 안되서 사진으로 했었는데 깃허브 블로그에서는 가능하다 이거 다 바꿔야겠다.

TID

• Determinant 계산식
• 종만북17장
• 밑바닥2 6장

TODO list

• 사진 latex 문법으로 교체
• 종만북-Algospot 1문제 이상 풀기
• 밑바닥2 6장 코드 이해하기

행렬식

Determinant

표기법

• 

• , 실수의 와는 다르게 결과값이 음수 일 수 있다.

성질

• 

• 

• 

• 인 행렬은 역행렬이 존재하지 않는다. 이 참이 되어야 하기 때문이다.

• 

• 

• 행렬 일 때,

• 

• 다음과 같은 성질을 다중선형성이라고 한다.

  1.

  ex)

  

  2.

  ex)

  

• 다음과 같은 성질을 교대성이라고한다.

  

  ex)

  

  상이 역전된다고 해석이 가능하다.

• , 여기서 n은 행렬 A의 차수.

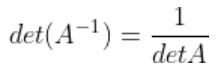
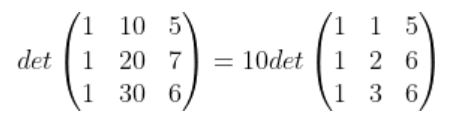
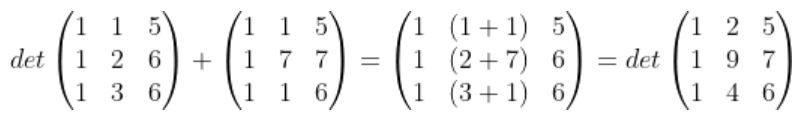
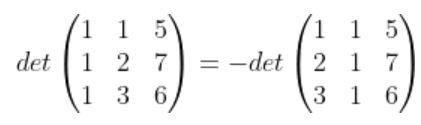
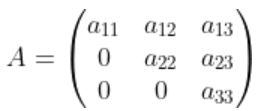• 로 표현되는 상삼각행렬(Upper triangular matrix) 또는 하삼각행렬 (lower triangular matrix) 일 경우

특징

• 실수 행렬의 행렬식은 실수이다. 복소 행렬의 행렬식은 일반적으로 복소수이다.

• 정방행렬이 아닌 행렬에서 행렬식은 정의되지 않는다.

행렬식 계산

행렬식은 다음과 같이 정의한다. \(det A = \sum_{i_{1},...,i_{n}} \epsilon_{i_{1}...i_{n}}a_{i_{1}1}...a_{i_{n}n}\) 여기서 랭크 \(\epsilon_{ijk}\)는 다음과 같이 정의한다.

• \(\epsilon_{123}=1\).
• 첨자가 바뀌면 -1을 곱한 것과 같다. \(\epsilon_{213}=-\epsilon_{123}=-1\) \(\epsilon_{312}=-\epsilon_{213}=\epsilon_{123}=1\)
• 첨자가 중복 인 경우는 0. \(\epsilon_{113}=\epsilon_{232}=\epsilon_{333}=0\)

특이 케이스에서의 행렬식 계산

블록대각

\(A=\begin{pmatrix}a_{11}&0&0\\0&a_{22}&a_{23}\\0&a_{32}&a_{33}\end{pmatrix}\)일 때, 행렬식은 다음과 같이 계산된다

\(detA=a_{11}det\begin{pmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{pmatrix}\).

블록삼각

블록 대각의 확장이라고 생각하면 된다.

\(A=\begin{pmatrix}a_{11}&a_{12}&...&a_{1n}\\0\\...&&A'\\0\end{pmatrix}\)일 때, 행렬식은 다음과 같이 계산된다.

\(det A=a_{11}detA'\).

일반적인경우 \(det\begin{pmatrix}2&1&3&2\\6&6&10&7\\2&7&6&6\\4&5&10&9\end{pmatrix}\\ \Rightarrow det\begin{pmatrix}2&1&3&2\\0&3&1&1\\0&6&3&4\\0&3&4&5\end{pmatrix}\\ \Rightarrow 2det\begin{pmatrix}3&1&1\\6&3&4\\3&4&5\end{pmatrix}\\ \Rightarrow 2det\begin{pmatrix}3&1&1\\0&1&2\\0&3&4\end{pmatrix}\\ =2\times3det\begin{pmatrix}1&2\\3&4\end{pmatrix} =2\times3\times(1\times4-2\times3)=12\)

20/05/03

기존의 TIL 용으로 쓰던 repository를 github 블로그로 만들었다.

좀더 깔끔 할 줄 알았는데 크기, 굵기 이런게 마크다운과 느낌이 사뭇다르다.

html 언어나 liquid 언어를 할 줄 몰라서 엄청 고생했다.

특히 카테고리 만드는 부분에서 시간을 엄청 잡아 먹었다.

하도 삽질하다보니 커밋수가 지붕을 뚫고 있다.

내일부터는 다시 제대로 공부하고 포스팅 해야겠다.

TODO list

• 밑바닥부터시작하는딥러닝2 6장
• 선형대수 1.3.4 까지
• 알고스팟 1문제 풀기

전치행렬

Transpose Matrix

표기법

성질

• 
• 
• 

• 단, D는 대각행렬이다.

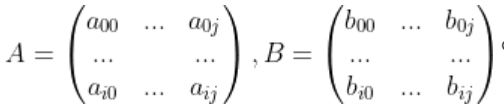일 때, 다음을 만족하는 경우 B는 A의 전치행렬(Transpose Matrix)이다.

즉,