Determinant
표기법
-
-
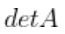
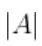, 실수의 
와는 다르게 결과값이 음수 일 수 있다.
성질
-
-
-
-
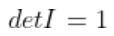
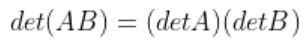
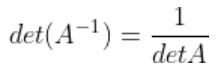
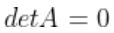인 행렬은 역행렬이 존재하지 않는다. 
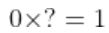이 참이 되어야 하기 때문이다. -
-
-
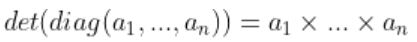
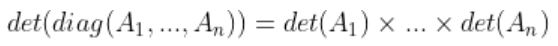
행렬
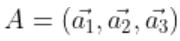일 때,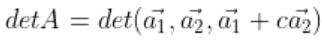 
-
-
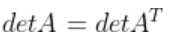
다음과 같은 성질을 다중선형성이라고 한다.
1.
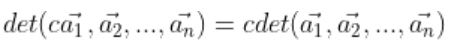
ex)
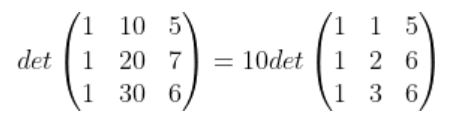
2.
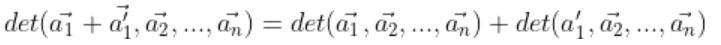
ex)
-
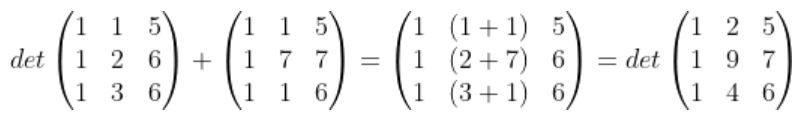
다음과 같은 성질을 교대성이라고한다.
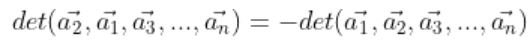
ex)
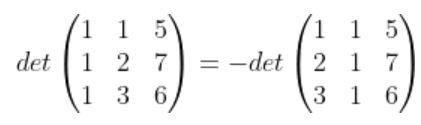
상이 역전된다고 해석이 가능하다.
-
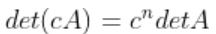, 여기서 n은 행렬 A의 차수. -
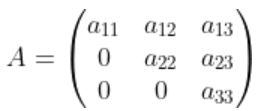로 표현되는 상삼각행렬(Upper triangular matrix) 또는 하삼각행렬 (lower triangular matrix) 일 경우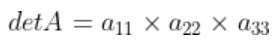 
특징
-
실수 행렬의 행렬식은 실수이다. 복소 행렬의 행렬식은 일반적으로 복소수이다.
-
정방행렬이 아닌 행렬에서 행렬식은 정의되지 않는다.
행렬식 계산
행렬식은 다음과 같이 정의한다. \(det A = \sum_{i_{1},...,i_{n}} \epsilon_{i_{1}...i_{n}}a_{i_{1}1}...a_{i_{n}n}\) 여기서 랭크 \(\epsilon_{ijk}\)는 다음과 같이 정의한다.
- \(\epsilon_{123}=1\).
- 첨자가 바뀌면 -1을 곱한 것과 같다. \(\epsilon_{213}=-\epsilon_{123}=-1\) \(\epsilon_{312}=-\epsilon_{213}=\epsilon_{123}=1\)
- 첨자가 중복 인 경우는 0. \(\epsilon_{113}=\epsilon_{232}=\epsilon_{333}=0\)
특이 케이스에서의 행렬식 계산
블록대각
\(A=\begin{pmatrix}a_{11}&0&0\\0&a_{22}&a_{23}\\0&a_{32}&a_{33}\end{pmatrix}\)일 때, 행렬식은 다음과 같이 계산된다
\(detA=a_{11}det\begin{pmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{pmatrix}\).
블록삼각
블록 대각의 확장이라고 생각하면 된다.
\(A=\begin{pmatrix}a_{11}&a_{12}&...&a_{1n}\\0\\...&&A'\\0\end{pmatrix}\)일 때, 행렬식은 다음과 같이 계산된다.
\(det A=a_{11}detA'\).
일반적인경우 \(det\begin{pmatrix}2&1&3&2\\6&6&10&7\\2&7&6&6\\4&5&10&9\end{pmatrix}\\ \Rightarrow det\begin{pmatrix}2&1&3&2\\0&3&1&1\\0&6&3&4\\0&3&4&5\end{pmatrix}\\ \Rightarrow 2det\begin{pmatrix}3&1&1\\6&3&4\\3&4&5\end{pmatrix}\\ \Rightarrow 2det\begin{pmatrix}3&1&1\\0&1&2\\0&3&4\end{pmatrix}\\ =2\times3det\begin{pmatrix}1&2\\3&4\end{pmatrix} =2\times3\times(1\times4-2\times3)=12\)
Comments