선형 회귀
일반적으로 선형 모델은 입력 특성의 가중치(weight) 합과 편향(bias)이라는 상수를 더해 예측을 만든다. \(\hat{y}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}\)
- \(\hat{y}\) : 예측값
- \(n\) : 특성의 개수
- \(x_{i}\) : \(i\)번째 특성값
- \(\theta_{j}\) : \(j\)번째 모델 파라미터 (편향 \(\theta_{0}\)과 특성의 가중치 \(\theta_{1},\theta_{2},..,\theta_{n}\) 포함).
- \(\theta\) : 편향 \(\theta_{0}\)과 \(\theta_{1}\)에서 \(\theta_{n}\)까지의 특성 가중치를 담은 모델의 파라미터 벡터.
- \(\mathbf{x}\) : \(x_{0}\)에서 \(x_{n}\)까지 담은 샘플의 특성 벡터입니다. \(x_{0}\)는 항상 1이다(편향을 미지수가 아닌 상수로 두기 위해서).
- \(\theta \cdot \mathbf{x}\) : 벡터 \(\theta\)와 \(\mathbf{x}\)의 점곱이다. 이는 \(\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}\)와 같다.
- \(h_{\theta}\)는 모델 파라미터 \(\theta\)를 사용한 가설(hypothesis) 함수이다.
모델을 훈련시킨다는 것은 모델이 훈련 세트에 가장 잘 맞도록 모델 파라미터를 설정하는 것이다. 이를 위해 먼저 모델이 훈련 데이터에 얼마나 잘 들어맞는지 측정해야 한다.
훈련 세트 \(\mathbf{X}\)에 대한 선형 회귀 가설 \(h_{0}\)의 MSE는 다음과 같이 계산한다. \(MSE(\mathbf{X},h_{0})=\frac{1}{m}\sum^m_{i=1}(\theta^{T}\mathbf{x}^{(i)}-y^{(i)})^{2}\) 지금의 식에서는 모델이 파라미터 벡터 \(\theta\)를 가지는 것을 명확히 하려고 이렇게 표현한 것이다 이후에는 MSE(\(\theta\))로 표기된다.
1.정규방정식
비용 함수를 최소화하는 \(\theta\)값을 찾기 위한 해석적인 방법이 있다. 바로 정규 방정식(Normal equation)이다. \(\hat{\theta}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}\)
- \(\hat{\theta}\)는 비용 함수를 최소화하는 \(\theta\) 값이다.
- \(\mathbf{y}\)는 \(y^{(1)}\)부터 \(y^{(m)}\)까지 포함하는 타겟 벡터이다.
먼저 공식을 테스트하기 위해 선형처럼 보이는 데이터를 생성하자
import numpy as np
import matplotlib.pyplot as plt
X=2*np.random.rand(100,1)
y=4+3*X+np.random.randn(100,1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()
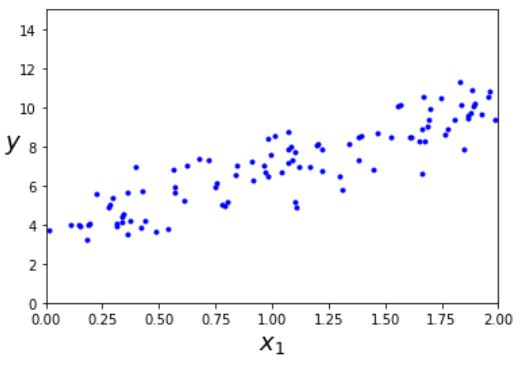
이 데이터를 생성하기 위해 사용한 함수는 \(y=4_3x_{1}+가우시안잡음\)이다. 정규방정식을 사용해 \(\hat{\theta}\)을 계산해보자. 먼저 역행렬을 계산하고 행렬곱셈을 한다.
>>> X_b = np.c_[np.ones((100,1)),X]
>>> theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
>>> theta_best
array([[3.57500712],
[3.28791026]])
rand를 써서 책과는 다른 값이 나올 수 있다. 우리는 원래의 기울기(\(x\)절편)와 편향(\(y\)절편)
이 각각 \(\theta_{0}\)=4와 \(\theta_{1}=3\)을 기대했었다. 하지만 잡음 때문에 원래 함수의 파라미터를 정확하게 재현하지는 못했다.
\(\hat{\theta}\)를 사용해 예측을 해보자. \(y_{predict} = x_{new_b} \cdot \theta_{best}\)를 한것이다.
>>> X_new = np.array([[0],[2]])
>>> X_new_b = np.c_[np.ones((2,1)),X_new]
>>> y_predict = X_new_b.dot(theta_best)
>>> y_predict
array([[ 3.57500712],
[10.15082764]])
모델의 예측을 그래프로 그리면 다음과 같다.
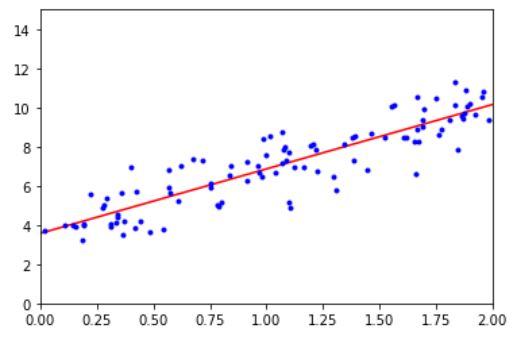
사이킷런에서는 간단하게 선형 회귀를 수행 할 수 있다.
>>> from sklearn.linear_model import LinearRegression
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X,y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([3.57500712]), array([[3.28791026]]))
>>> lin_reg.predict(X_new)
array([[ 3.57500712],
[10.15082764]])
intercept_에는 y절편(bias), coef에는 x절편(기울기)값이 들어 있다.
LinearRegression 클래스는 scipy.linalg.lstsq() 함수(‘최소 제곱(least squares)’에서 따왔다)를 기반으로 한다. 이 함수를 직접 호출할 수도 있다.
>>> theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b,y,rcond= 1e-6)
>>> theta_best_svd
array([[3.57500712],
[3.28791026]])
이 함수는 \(\hat{\theta}=\mathbf{X}^{+}\mathbf{y}\)을 계산한다. 여기서 \(\mathbf{X}^{+}\)는 \(\mathbf{X}\)의 유사역행렬(pseudoinverse, 혹은 무어-펜로즈(Moore-Penrose)역행렬)이다.
np.linalg.pinv() 함수를 사용하면 유사역행렬을 직접 구할 수 있다.
>>> np.linalg.pinv(X_b).dot(y)
array([[3.57500712],
[3.28791026]])
유사역행렬 자체는 특잇값 분해(Singular Value Decomposition, SVD)라 부르는 표준 행렬 분해 기법을 사용해 계산된다. SVD는 훈련 세트 행렬 \(\mathbf{X}\)를 3개의 행렬 곱셈 \(\mathbf{U \Sigma V^{T}}\)로 분해한다. 유사역행렬은 \(\mathbf{X^{+}=V \Sigma^{+} U^{T}}\)로 계산된다. \(\mathbf{\Sigma^{+}}\)를 계산하기 위해 알고리즘이 \(\mathbf{\Sigma}\)를 먼저 구하고 그다음 어떤 낮은 임계값보다 작은 모든 수를 0으로 바꾼다. 그 다음 0이 아닌 모든 값을 역수로 치환한다. 마지막으로 만들어진 행렬을 전치한다. 정규방정식을 계산하는 것보다 이 방식이 훨씬 효율적이다. 원래 \(\mathbf{X}\)이 특이행렬이 아닐 때 정규방정식이 작동하지 않지만 유사역행렬을 사용하면 항상 구할 수 있다.
2.계산 복잡도
정규방정식은 \((n+1) \times (n+1)\) 크기가 되는 \(\mathbf{X^{T}X}\)의 역행렬을 계산합니다. 역행렬을 계산하는 계산 복잡도(Computational complexity)는 일반적으로 \(O(n^{2.4})\)에서 \(O(n^{3})\) 사이이다. 다시 말해 특성 수가 두 배로 늘어나면 계산 시간이 대략 \(2^{2.4}=5.3\)에서 \(2^{3}=8\)배로 증가한다.
사이킷런의 LinearRegression class가 사용하는 SVD 방법은 약 \(O(n^2)\)이다. 특성의 개수가 두배로 늘어나면 계산 시간이 대략 4배가 된다.
학습된 선형 회귀 모델은 예측이 매우 빠르다. 예측 계산 복잡도는 샘플 수와 특성 수에 선형적이다. 즉 예측하려는 샘플이 두 배로 늘어나면 걸리는 시간도 거의 두 배 증가한다.
다음의 방식들은 훈련 샘플이 너무 많아 메모리에 모두 담을 수 없을 때 적합한 방식이다.
경사 하강법
경사 하강법(Gradient descent, GD)은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘이다. 경사 하강법의 기본 아이디어는 비용 함수를 최소화 하기 위해 반복해서 파라미터를 조정해가는 것이다.
경사 하강법은 기울기가 가장 가파른 방향으로 나아가는 방법이다. 파라미터 벡터 \(\theta\)에 대해 비용 함수의 현재 gradient를 계산한다. 그리고 gradient가 감소하는 방향으로 진행한다. gradient가 0이 되면 최소값에 도달한 것이다.
구체적으로 보면 \(\theta\)를 임의의 값으로 시작해서 한 번에 조금씩 비용 함수가 감소되는 방향으로 진행하여 알고리즘이 최소값에 수렴할 때까지 점진적으로 향상시킨다.
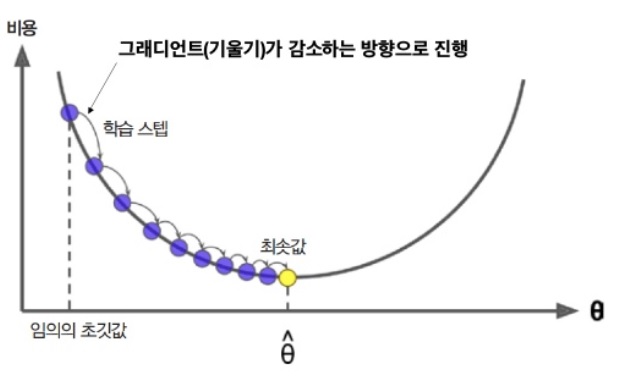
경사 하강법에서 중요한 파라미터는 step의 크기로, 학습률(Learning rate) 하이퍼파라미터로 결정된다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸린다.
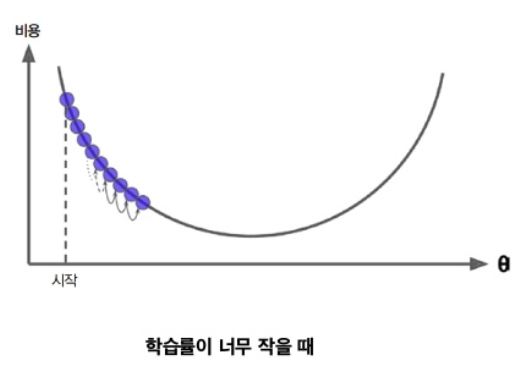
한편 학습률이 너무 크면 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 높은 곳으로 올라가게 될지도 모른다. 이는 알고리즘을 더 큰 값으로 발산하게 만들어 적절한 해법을 찾지 못하게 한다.
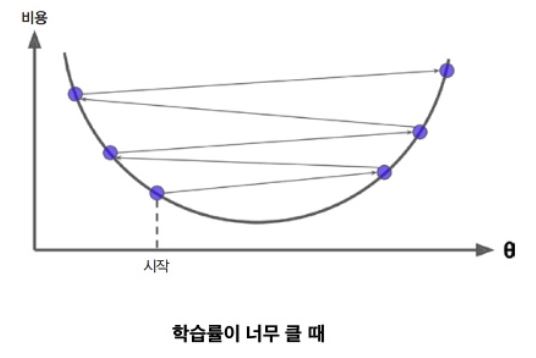
다음 그림은 2개의 문제를 보여준다.
첫째, 왼쪽에서 시작하면 경사하강법이 전역 최소값(global minimum) 보다 덜 좋은 지역 최소값(local minimum)에 수렴할 수 도 있다.
둘째, 오른쪽에서 시작하면 기울이가 0에 가까운 지역을 지나기 위해 시간이 오래 걸리고 일찍 멈추게 되어 global minima에 도달하지 못한다.
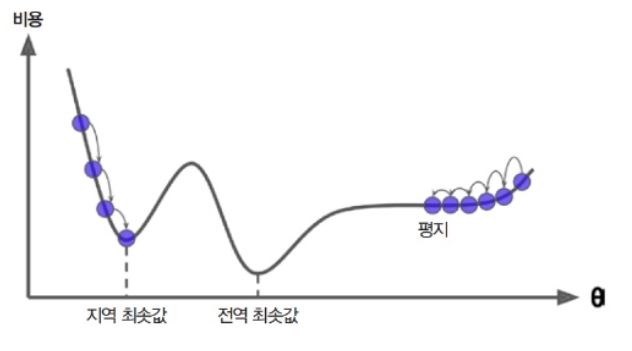
다행히 선형 회귀를 위한 MSE 비용 함수는 곡선에서 어떤 두 점을 선택해 선을 그어도 곡선을 가로지르지 않는 볼록 함수(Convex function)이다. 이는 local minima 없이 global minima만 존재 한다는 것이다. 또한 연속된 함수이고 기울기가 갑자기 변하지 않는다.
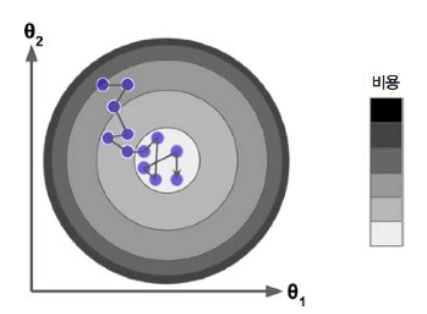
사실 특성들의 스케일이 매우 다르면 이렇게 그릇 모양이 아닌 길쭉한 모양일 수 있다.
다음 그림은 특성 1과 특성 2의 스케일이 같은 훈련 세트(왼쪽)와 특성 1이 특성 2보다 더 작은 훈련 세트(오른쪽)에 대한 경사 하강법을 보여준다.
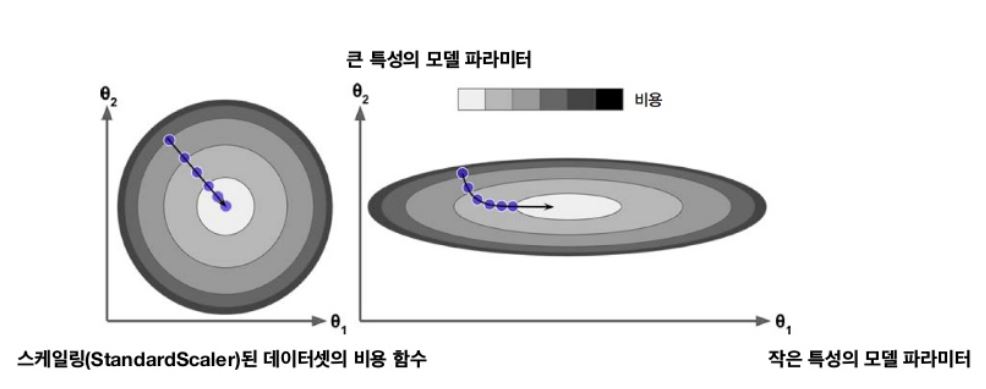
위의 사진에서 모델이 global minima에 수렴하기 위해 걸리는 시간이 다르다는 것을 알 수 있다. 그래서 경사 하강법을 사용할 때 모든 특성이 같은 스케일을 갖도록 만드는 것이 좋다. 또한, 모델 훈련이 비용함수를 최소화하는 모델 파라미터의 조합을 찾는 일인 것을 알 수 있는데 이를 모델의 파라미터 공간(Parameter space)에서 찾는다고 말한다. 모델이 가진 파라미터가 많을수록 이 공간의 차원은 커지고 검색은 더 어려워진다.
1.배치 경사 하강법
경사 하강법을 구현하려면 먼저 각 모델 파라미터 \(\theta_{j}\)에 대해 비용 함수의 gradient를 계산해야 한다. 다시 말해 모델 파라미터가 조금 변경될 때 비용 함수가 얼마나 바뀌는 지를 계산해야 한다. 이를 편도함수(Partial derivative)라고 한다. 다음 식은 파라미터 \(\theta_{j}\)에 대한 비용 함수의 편도함수 \({\partial \over \partial \theta_{j}}MSE(\theta)\)이다. \(MSE(\mathbf{\theta})=\frac{1}{m}\sum^m_{i=1}(\theta^{T}\mathbf{x}^{(i)}-y^{(i)})^{2} \\ {\partial \over \partial \theta_{j}}MSE(\theta)=\frac{2}{m} \sum^{m}_{i=1}(\theta^{T} \mathbf{x}^{(i)}-y^{(i)})x^{(i)}_{j}\) 편도함수를 각각 계산하는 대신 다음 식을 사용하면 한꺼번에 계산할 수 있다. gradient vector \(\nabla_{\theta}MSE(\theta)\)는 비용 함수의 편도함수를 모두 담고 있다. 이 함수를 배치 경사 하강법(Batch gradient descent)라고 한다.
\[\nabla_{\theta}MSE(\theta)=\begin{pmatrix}{ \partial \over \partial \theta_{0}}MSE(\theta) \\ {\partial \over \partial \theta_{1}}MSE(\theta) \\ ... \\ {\partial \over \partial \theta_{n}}MSE(\theta) \\ \end{pmatrix}=\frac{2}{m} \mathbf{X^{T} (X \theta - y)}\]새로운 파라미터는 이 방향의 반대로 가야한다. 여기서 학습률(Learning rate) \(\eta\)가 사용된다. 내려가는 스텝의 크기를 결정하기 위해 gradient 벡터에 \(\eta\)를 곱한다. \(\mathbf{\theta}^{(next \ step)} = \theta - \eta \nabla_{\theta}MSE(\theta)\) 이 알고리즘을 간단히 구현하면 다음과 같다.
>>> eta = 0.1
>>> n_iterations = 100
>>> m = 100
>>>
>>> theta = np.random.randn(2,1)
>>>
>>> for iteration in range(n_iterations):
>>> gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y)
>>> theta = theta - eta * gradients
>>> theta
array([[3.87460118],
[3.14424413]])
정규방정식으로 찾은 것과 정확히 같은 값이 나온다.
이번에는 leraning rate를 바꿔서 확인해 보자.
theta_path_bgd = []
def plot_gradient_descent(theta, eta, theta_path=None):
m = len(X_b)
plt.plot(X, y, "b.")
n_iterations = 1000
for iteration in range(n_iterations):
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-" if iteration > 0 else "r--"
plt.plot(X_new, y_predict, style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
plt.title(r"$\eta = {}$".format(eta), fontsize=16)
theta = np.random.randn(2,1)
plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
plt.show()
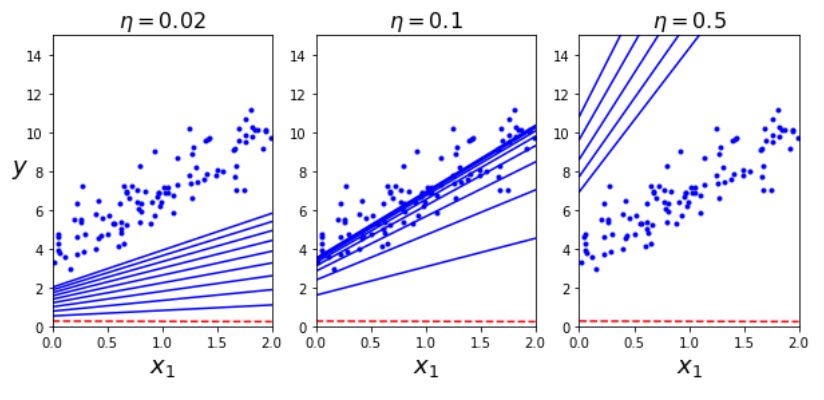
왼쪽의 학습률은 너무 낮다. 적절한 값을 내려면 아마 꽤 많은 학습시간을 소요할 것이다. 오른쪽은 학습률이 너무 높은 경우다 최적점에서 점점 더 멀어져 발산하게 되었다. 가운데가 가장 적절한 정도이다.
적절한 학습률을 찾으려면 그리드 탐색을 사용한다(2장). 하지만 그리드 탐색에서 수렴하는 데 너무 오래 걸리는 모델을 막기 위해 반복 횟수를 제한해야 한다.
여기서 반복 횟수를 지정하는 방식은 일단 횟수를 엄청 크게 하고 미리 허용오차(tolerance) \(\varepsilon\)를 지정한 후 gradient vector의 norm이 이 값 보다 작아지면 알고리즘을 종료하는 것이다.
2.확률적 경사 하강법
배치 경사 하강법의 가장 큰 문제는 매 스텝에서 전체 훈련 세트를 사용해 gradient를 계산하기 때문에 훈련 세트가 커질수록 느려지는 것이다. 이와 반대로 확률적 경사 하강법(Stochastic Gradient Descent, SGD)은 매 스텝에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 gradient를 계산한다. 한 번에 하나의 샘플을 처리하기 때문에 이전보다 더 빠르다.
반면에 확률적이기 떄문에 배치 경사 하강법보다 불안정 하다. 비용함수가 최소값에 다다를 떄까지 안정적으로 감소하지 않고 위아래로 요동치면서 평균적으로 감소한다. 시간이 지나면 최소값에 매우 근접하겠지만 요동이 지속되면서 최소값에 안착하지 못할 것이다. 알고리즘이 멈출 때의 파라미터가 최적치는 아니다.
비용 함수가 불규칙할 경우 알고리즘이 local minima 건너뛸 수 있도록 도와주므로 global minima에 접근할 확률이 늘어난다.
local minima에 덜 취약한 것은 좋지만 global minima에 안착하지 못한다는 점에서는 좋지 않다. 하나의 해결 방법은 학습률을 점진적으로 감소 시키는 것이다. 이 과정은 금속공학 분야에서 가열한 금속을 천천히 냉각시키는 풀림(Annealing)과정에서 영감을 얻은 담금질 기법(Simulated annealing) 알고리즘과 유사하다. 매 반복에서 학습률을 결정하는 함수를 학습 스케줄(Learning schedule)라고 부른다. 학습률에 관한 문제는 이전과 같으므로 적절한 값을 찾는게 중요하다.
다음 코드는 간단한 학습 스케줄을 사용한 SGD의 구현이다.
>>> n_epochs = 50
>>> theta_path_sgd = []
>>> m = len(X_b)
>>> t0, t1 = 5, 50 # 여기가 학습 스케줄 하이퍼파라미터
>>> def learning_schedule(t):
>>> return t0/(t+t1)
>>>
>>> theta = np.random.randn(2,1)
>>>
>>> for epoch in range(n_epochs):
>>> for i in range(m):
>>> if epoch == 0 and i < 20:
>>> y_predict = X_new_b.dot(theta)
>>> style = "b-" if i > 0 else "r--"
>>> plt.plot(X_new, y_predict, style)
>>> random_index = np.random.randint(m)
>>> xi = X_b[random_index:random_index+1]
>>> yi = y[random_index:random_index+1]
>>> gradients = 2 * xi.T.dot(xi.dot(theta)-yi)
>>> eta = learning_schedule(epoch*m+i)
>>> theta = theta - eta *gradients
>>> theta_path_sgd.append(theta)
>>> theta
array([[3.93429656],
[3.15150671]])
>>> plt.plot(X, y, "b.")
>>> plt.xlabel("$x_1$", fontsize=18)
>>> plt.ylabel("$y$", rotation=0, fontsize=18)
>>> plt.axis([0, 2, 0, 15])
>>> plt.show()
한 데이터 세트를 모두 돌았을 때를 기준으로 1에포크(epoch)라고 한다. 즉 이 코드는 전체 데이터 세트에 대해 50번 학습을 한 것이다.
다음 그림은 훈련 스텝의 첫 20개를 보여준다. step이 불규칙하게 진행하는 것을 확인할 수 있다.
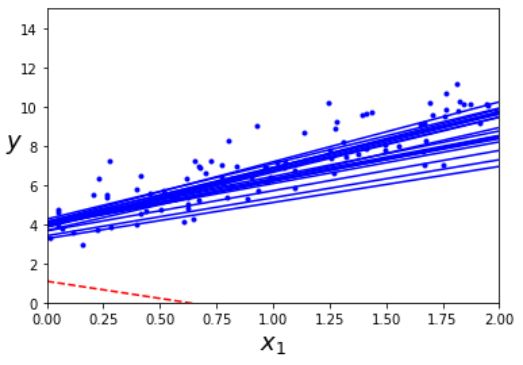
사이킷런에서 SGD 방식으로 선형 회귀를 사용하려면 기본값으로 제곱 오차 비용 함수를 최적화하는 SGDRegressor 클래스를 사용한다.
>>> from sklearn.linear_model import SGDRegressor
>>> sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
>>> ## max_iter= epoch, tol = 허용오차, penalty = 규체, eta = 학습률
>>> sgd_reg.fit(X,y.ravel())
>>> sgd_reg.intercept_,sgd_reg.coef_
(array([3.87484114]), array([3.0835934]))
3.미니배치 경사 하강법
마지막은 미니배치 경사 하강법(Mini-batch gradient descent)이다. 미니배치는 임의의 작은 샘플 세트이다. 이 작은 샘플 세트에 대해 진행함으로써 GPU와 같은 행렬 연산에 최적화된 하드웨어를 통해 성능 향상을 얻는다.
미니배치를 어느 정도 크게 하면 이 알고리즘은 파라미터 공간에서 SGD보다 덜 불규칙 하게 움직인다. SGD보다 최소값에 더 가까이 가지만 local minima에는 조금 더 민감하다.
예제는 다음과같다.
>>> theta_path_mgd = []
>>>
>>> n_iterations = 50
>>> minibatch_size = 20
>>>
>>> np.random.seed(42)
>>> theta = np.random.randn(2,1) # 랜덤 초기화
>>>
>>> t0, t1 = 200, 1000
>>> def learning_schedule(t):
>>> return t0 / (t + t1)
>>>
>>> t = 0
>>> for epoch in range(n_iterations):
>>> shuffled_indices = np.random.permutation(m)
>>> X_b_shuffled = X_b[shuffled_indices]
>>> y_shuffled = y[shuffled_indices]
>>> for i in range(0, m, minibatch_size):
>>> t += 1
>>> xi = X_b_shuffled[i:i+minibatch_size]
>>> yi = y_shuffled[i:i+minibatch_size]
>>> gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
>>> eta = learning_schedule(t)
>>> theta = theta - eta * gradients
>>> theta_path_mgd.append(theta)
>>> theta
array([[3.94654401],
[3.15293798]])
참고로 미니배치를 훈련 세트 전체로 하면 배치 경사 하강법과 똑같이 된다.
다음 그림은 세가지 경사 하강법 알고리즘이 훈련 과정 동안 파라미터 공간에서 움직인 경로이다.
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(7,4))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1, label="Stochastic")
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2, label="Mini-batch")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3, label="Batch")
plt.legend(loc="upper left", fontsize=16)
plt.xlabel(r"$\theta_0$", fontsize=20)
plt.ylabel(r"$\theta_1$ ", fontsize=20, rotation=0)
plt.axis([2.5, 4.5, 2.3, 3.9])
plt.show()
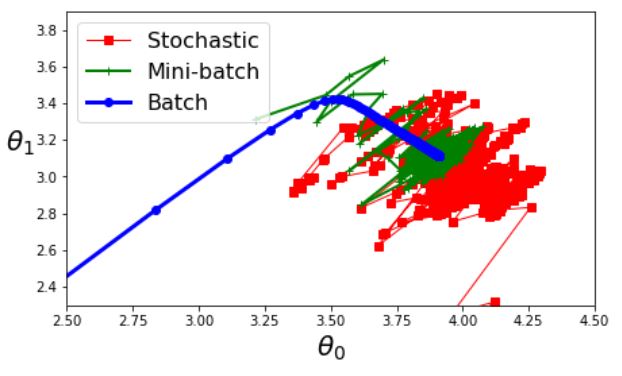
모두 최소값 근처에 도달했지만 배치 경사 하강법 빼고는 실제 최소값 근처에서 맴돈다. 하지만 배치 경사 하강법은 너무 많은 시간이 소요되고, 확률적 경사 하강법과 미니배치 경사 하강법도 적절한 학습 스케줄을 사용하면 최소값에 도달한다.
아래의 표는 지금까지 논의한 알고리즘을 선형회귀를 사용해 비교한 표이다.
| 알고리즘 | m이 클 때 | 외부 메모리 학습 지원 | n이 클 때 | 하이퍼 파라미터 수 | 스케일 조정 필요 | 사이킷런 |
|---|---|---|---|---|---|---|
| 정규 방정식 | 빠름 | N | 느림 | 0 | N | N/A |
| SVD | 빠름 | N | 느림 | 0 | N | LinearRegression |
| 배치 경사 하강법 | 느림 | N | 빠름 | 2 | Y | SGDRegressor |
| 확률적 경사 하강법 | 빠름 | Y | 빠름 | \(\ge 2\) | Y | SGDRegressor |
| 미니배치 경사 하강법 | 빠름 | Y | 빠름 | \(\ge 2\) | Y | SGDRegressor |
다항 회귀
선형 모델은 비선형 데이터를 학습하는 데에도 사용할 수 있다. 간단한 방법은 각 특성의 제곱을 새로운 특성으로 추가하고, 이 확장된 특성을 포함한 데이터셋에 선형 모델을 훈련시키는 것이다. 이런 기법을 다항 회귀(Polynomial regression)라고 한다.
먼저 간단한 2차 방정식(Quadratic equation)으로 잡음이 포함된 비선형 데이터를 생성한다.
m=100
X=6*np.random.rand(m,1)-3
y=0.5*X**2+X+2+np.random.randn(m,1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()
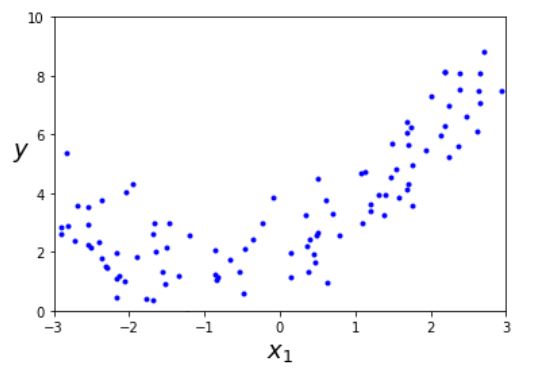
훈련 데이터의 변환은 사이킷런의 PolynomialFeatrues를 사용해 각 특성을 제곱 하여 새로운 특성을 추가할 것이다.
>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly_features = PolynomialFeatures(degree=2, include_bias=False)
>>> X_poly = poly_features.fit_transform(X)
>>> X[0]
array([2.64919746])
>>> X_poly[0]
array([2.64919746, 7.01824719])
이제 이 확장된 훈련 데이터에 Linear Regression을 적용해 보자
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X_poly,y)
>>> lin_reg.intercept_,lin_reg.coef_
(array([2.08525638]), array([[0.97095511, 0.44344077]]))
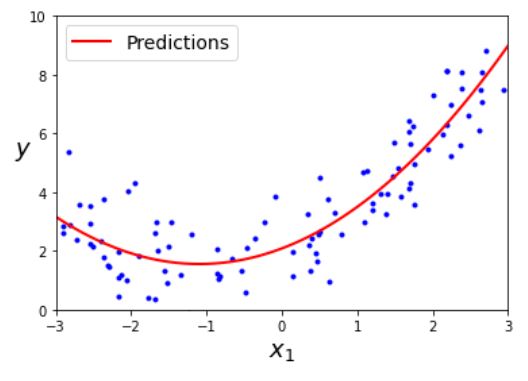
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
plt.show()
PolynomialFeatrues는 주어진 차수까지 특성 간의 모든 교차항을 추가한다.
예를들어 degree=3일 때 \(a^{2},a^{3},b^{2},b^{3},ab,a^{2}b,ab^{2}\) 모두 다 특성으로 추가한다.
Comments