비최대 억제(Non-Maximum Suppression)

24 Aug 2020 • Computer Vision

코드링크

비최대 억제(Non-Maximum Suppression)

이전에 포스팅한 모라벡, 해리스, 헤시안 행렬, 슈산 모두 어떤 점에 대해 특징일 가능성을 측정해주었다.
하지만 코너에서 한 점만 큰 값을 갖는 것이 아니라 큰 값이 일정한 범위에 퍼져있어 한 지점을 선택하는 방법이 필요하며 이러한 일을 위치 찾기(Localization)이라 부른다(SLAM 분야의 localization과는 다르다). 가장 합리적인 방법으로 지역 최대점을 취하는 것인데, 이름에서 알 수 있듯이 지역내에서 최대가 아니면 억제되고 지역내에서 최대라면 특징점으로 결정된다.
일반적으로 지역을 정할 때는 동서남북의 네 이웃 화소만 보는 4-연결 방식과 대각선을 포함한 8-연결 방식이 있다. 물론 상황에 따라 더 넓은 지역을 이웃으로 취급할 수도 있다.
지역내에서 최대값이더라도 특징점으로 보기 애매한 경우가 있다. 이를 위해 지역내에서 최대값이더라도 임계값을 설정하여 임계값보다 작은 경우 잡음(noise)로 취급한다.

brown은 특징점이 영상의 특정 부분에는 밀집되어 있고 다른 부분은 드물게 분포하는 문제를 해결하기 위해 특징점에 대해 지역 내에서 최대이며 주위 화소보다 일정 비율 이상 커야 한다는 조건을 만들었다. 이를 적응적 비최대 억제 방법(adaptive non-maximum suppression)이라고 한다.


코드 구현

이번 구현에서는 이전에 구현했던 harris corner를 이용해 특징점의 수가 얼마나 주는 지 확인 할 것이다.

from util import *
import matplotlib.pyplot as plt
import numpy as np
import cv2

img = cv2.imread('./data/red_deer.jpg',cv2.IMREAD_GRAYSCALE)
plt.imshow(img,cmap='gray')
plt.show()

우선 지역이 4-연결 구성일 때와 8-연결 구성일 때에 대해 구현하였으며 threshold는 임의로 지정하였다. 사실 이 구현에서는 harris를 검출할 때 임계값을 설정 했었기 때문에 이웃보다 크기만 하면 검출된다.

def NMS(feature,n=4,threshold=0.02):
    feature = np.expand_dims(feature,-1)
    
    # 상하좌우
    n_r = np.pad(feature[1:], ((0, 1), (0, 0),(0,0)))
    n_l = np.pad(feature[:-1], ((1, 0), (0, 0),(0,0)))
    n_d = np.pad(feature[:,1:], ((0, 0), (0, 1),(0,0)))
    n_u = np.pad(feature[:,:-1], ((0, 0), (1, 0),(0,0)))

    if n==8: # 대각선
        n_ul = np.pad(n_u[:-1], ((1, 0), (0, 0),(0,0)))
        n_ur = np.pad(n_u[1:], ((0, 1), (0, 0),(0,0)))
        n_dl = np.pad(n_d[:-1], ((1, 0), (0, 0),(0,0)))
        n_dr = np.pad(n_d[1:], ((0, 1), (0, 0),(0,0)))
        ret = np.concatenate([feature,n_r,n_l,n_d,n_u,n_ul,n_ur,n_dl,n_dr],axis=-1)
    else:
        ret = np.concatenate([feature,n_r,n_l,n_d,n_u],axis=-1)
    ret = np.expand_dims(np.argmax(ret,-1),-1) # 최대값을 가지는 index

    return np.squeeze(np.where(np.logical_and(ret==0,feature>threshold),feature,0)) # ret이 0 이라는 것은 지역보다 크다는 것을 뜻한다.

우선 NMS 적용전과 적용후의 그림이다.

harris = Harris_corner(img,threshold=0.02)
fig = plt.figure(figsize=(13,13))
plt.subplot(121)
plt.imshow(draw_featrue_point(img,harris,dot_size=5))
plt.xlabel('before NMS')

NMS_harris = NMS(harris)
plt.subplot(122)
plt.imshow(draw_featrue_point(img,NMS_harris,dot_size=5))
plt.xlabel('after NMS')
fig.tight_layout()
plt.show()

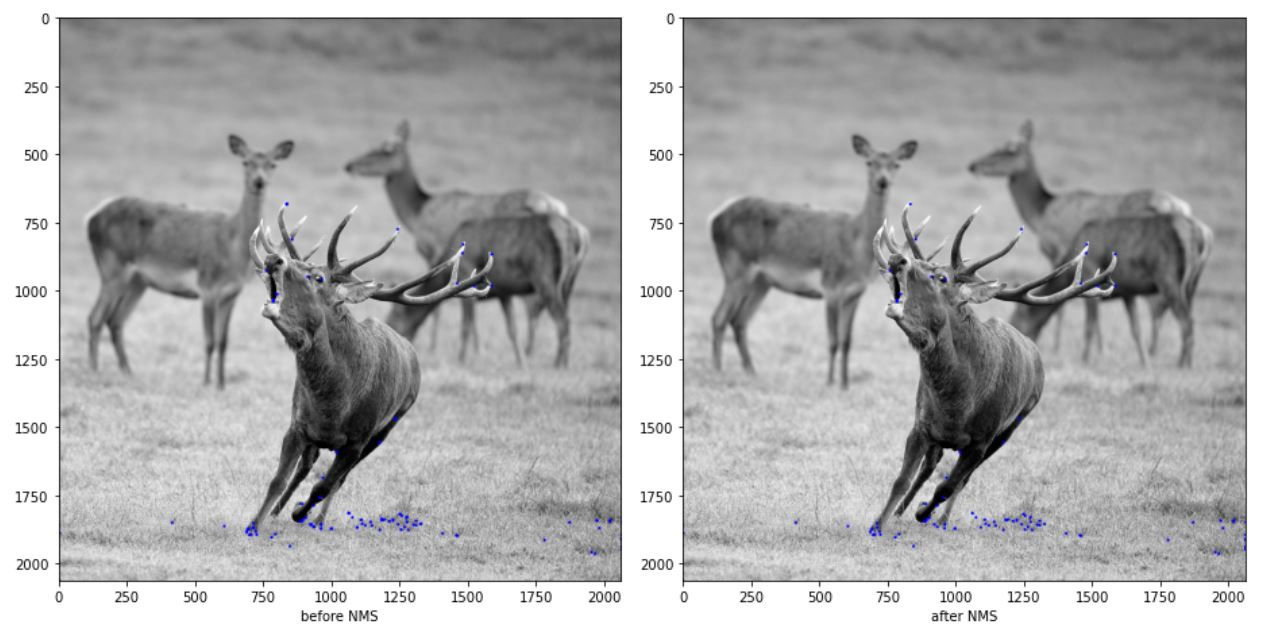
원의 굵기가 얇아진것 같기는 하지만 그림으로 봐서는 확실하게 줄어든지 잘 모르겠다. 확실하게 하기 위해 0보다 큰 값들을 카운팅해보자.

>>> print(np.sum(harris>0),np.sum(NMS_harris>0))
292 106

확실히 특징점의 갯수가 3배 가량 줄어 든 것을 확인할 수 있다.

Comments

Related Posts