ResNet

ResNet은 2015 ILSVRC, COCO 대회에서 우승한 모델이며 특히 3.6%의 top-5 error를 달성함으로써 사람의 분류 기준인 5% 내외를 뛰어 넘었다.

Introduction

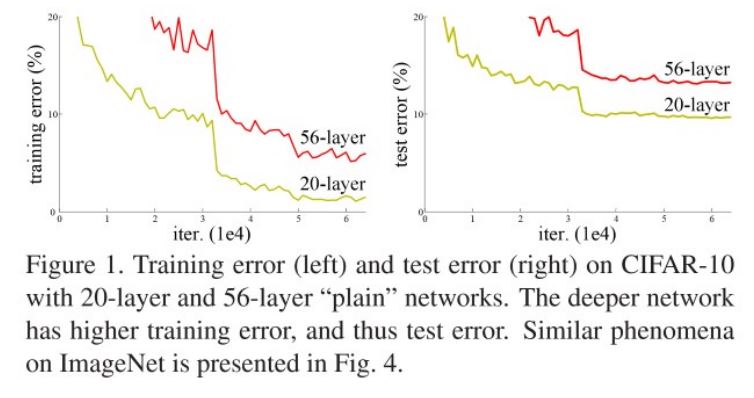
이전의 VGG,GoogleNet, Batch Normalization 등을 통해 모델의 깊이가 깊어졌지만 위의 사진처럼 모델의 깊이가 어느정도 깊어졌을 때 오히려 training과 test error가 늘어났다. 이러한 현상을 논문에서 “Degradation Problem”이라고 언급한다. 저자는 실험을 통해 overfitting에 의해 발생하는 문제가 아님을 밝히고 Degradation 문제에 집중해 Residual learning을 소개한다.

Residual Learning

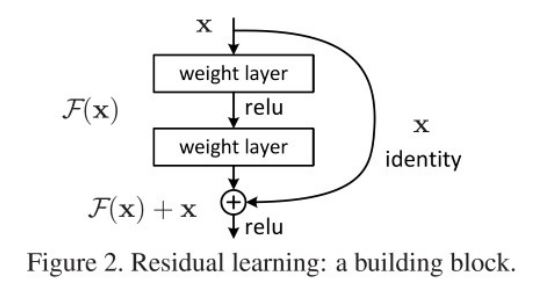
Residual Learing의 기본아이디어는 잔차(Residual)에 대해 학습하는 것이다.
기존의 모델에서는 입력 x에 대해 \(\mathcal{H}(x)\)가 정답이 되게끔 학습을 했다면 Residual Learning은 \(\mathcal{F}(x)+x\)가 정답이 되게끔 학습하는 방식이다. 다시 말하자면 입력 x가 정답이 되기 위해 부족한 부분(\(\mathcal{F}(x)\), 잔차)을 배우는 것이다.

여기서 주의할 점은 사진에서 layer를 두 개로 쌓았다는 것이다. 두 개 이상일 경우 Relu에 의해 비선형성이 되지만 한 개일 경우 linear 함수와 동일하기 때문에 아무 소용이없다.

Resiaul Learning을 식으로 표현하면 다음과 같이 되는데,

\[y = \mathcal{F}(x,\left\{ W_{i}\right\}) + x\]

이 식을 논문에서는 Identity Mapping이라고 표현한다. 하지만 이 식의 경우 \(x\)와 \(\mathcal{F}(x)\)의 shape이 맞지 않을 경우 문제가 된다. 이 경우에는 추가적인 파라미터가 들어가고 식은 다음과 같이 된다.

\[y=\mathcal{F}(x,\left\{ W_{i} \right\})+W_{s}x\]

이 식을 논문에서 Projection shortcut이라 표현한다. CNN에서는 1x1 convolution을 이용해 shape을 맞춘다.

Network Architectures

아래의 표는 ResNet에 대한 세부사항을 보여준다.

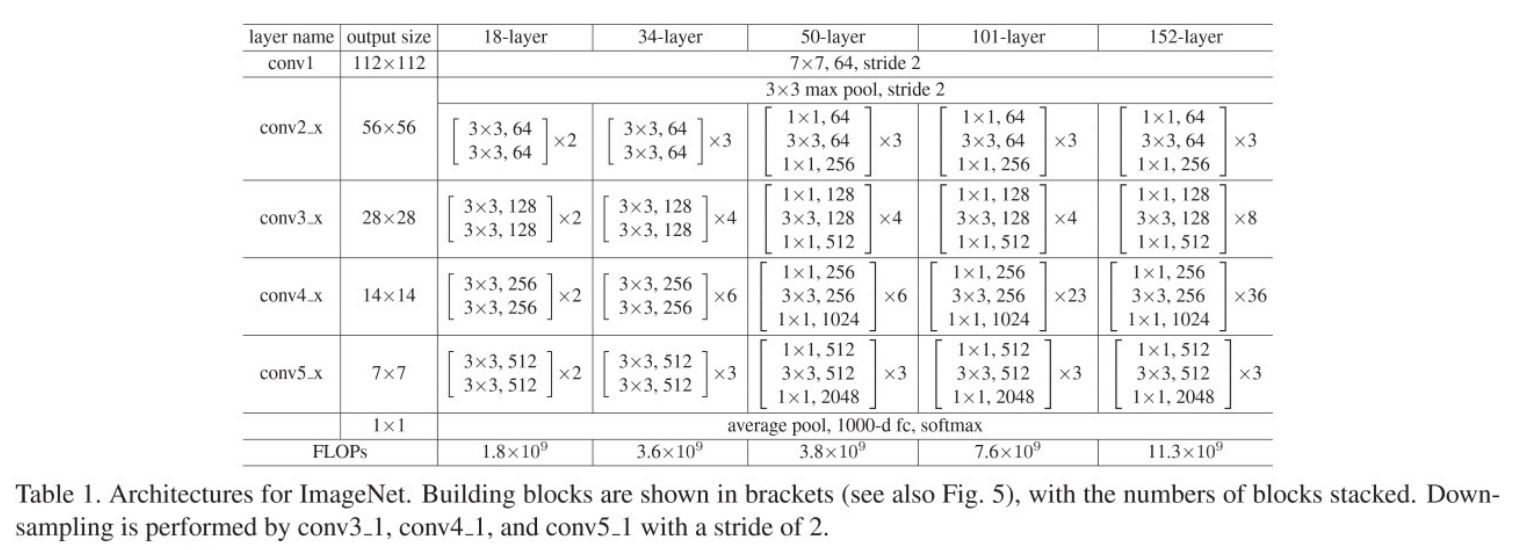
사실 이 표만으로는 정확히 이해하기 힘든데 아래의 사진을 보자.

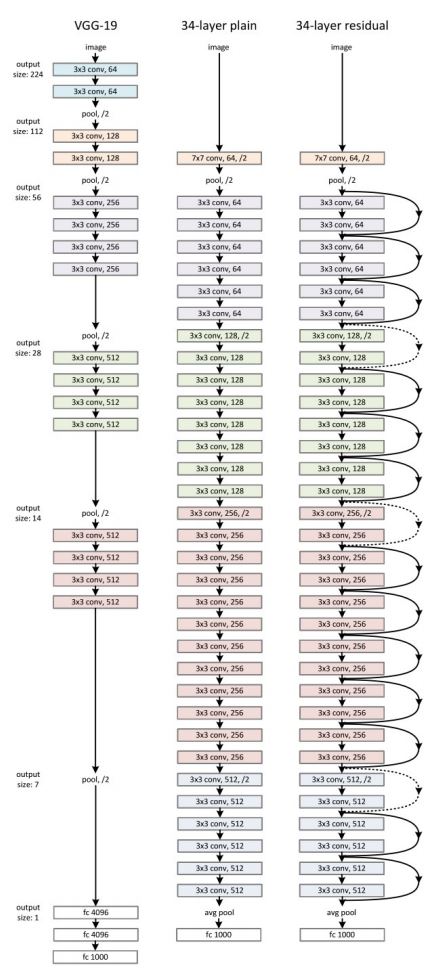
제일 오른쪽에 있는 모델이 ResNet 34-layer이다. 모델에서 실선으로 포물선을 그리는 화살표가 Identity Mapping에 해당하며 점선으로 포물선을 그리는 화살표가 Shape을 맞추기 위해 Projection shortcut을 사용한 부분에 해당한다. 그림에서 /2는 stride를 2로 주었다는 것을 의미하며 이때 Projection shortcut에 사용되는 커널의 사이즈는 그대로 1x1이지만 stride는 2로 설정되어 Down sampling을 수행한다.

50-layer 부터는 한 block이 1x1, 3x3, 1x1 크기의 커널이 순서대로 있는 것을 볼 수 있는데 여기서 하나를 더 주목하자면 conv2_x의 첫 block의 output은 256개 였다가 다음 block에서 첫 1x1의 output은 64개이다. 즉 차원을 감소시켜 parameter의 수를 조절한 것으로 볼 수 있다. 이러한 방식은 이전의 GoogLeNet에서 볼 수 있는 방식이다.
이 block 구조를 “Bottleneck” 구조라고 한다. 이 구조로 얻은 이득은 위 표의 18-layer와 34-layer, 50-layer의 FLOPs를 보면 알 수 있다.

Experiments

ImageNet Classification

아래의 그래프와 표는 1000개의 class를 가지는 ImageNet 2012 classification dataset으로 Plain net과 ResNet에 대해 error를 측정한 결과이다.

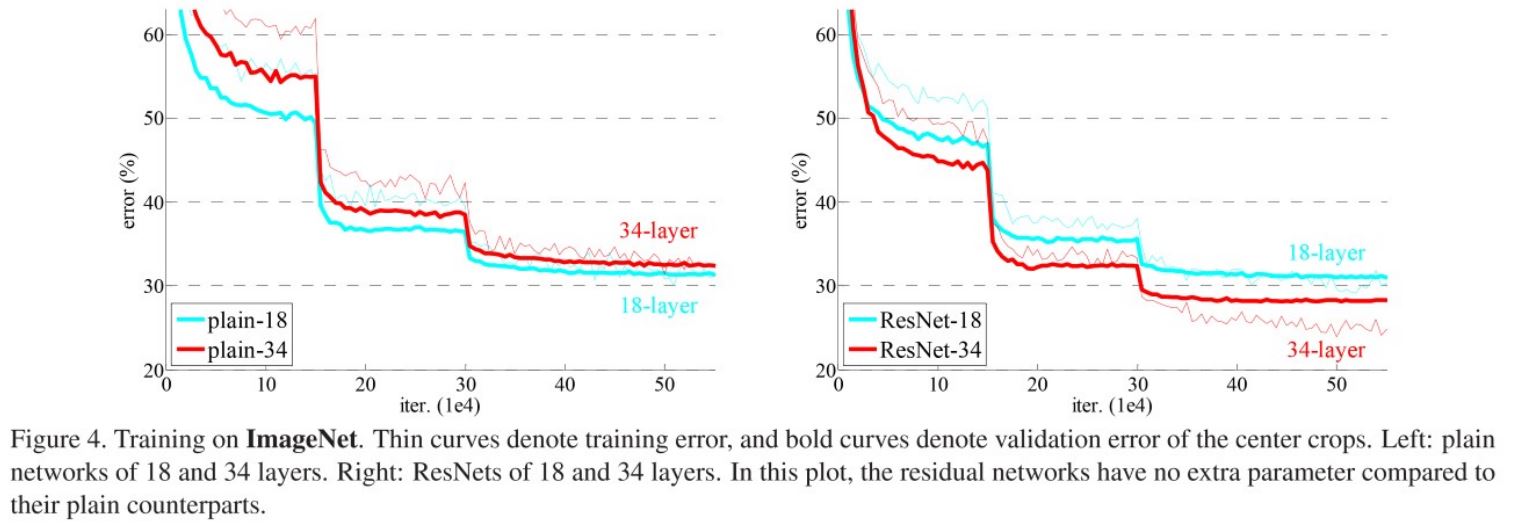
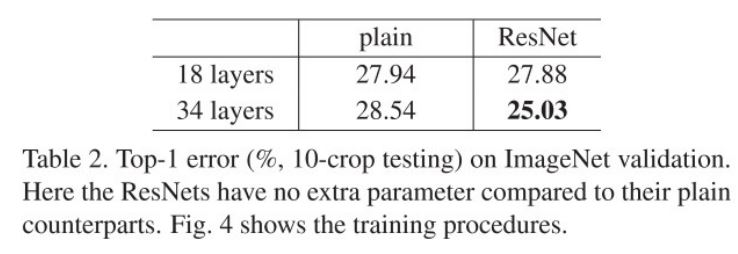
왼쪽의 그래프(Plain)를 보면 모델의 깊이가 깊은데도 불구하고 34-layer가 더 나쁜 성능을 보인다(Degradation problem). 심지어 Plain 모델은 BatchNormalization도 적용이 되어있으며 그래프를 보면 loss가 점점 줄어들고 있기 때문에 gradient vanishing에 의한 문제도 아니다.

반면 오른쪽 그래프(ResNet)의 결과를 보면 확실히 34-layer는 18-layer에 비해 성능이 좋으며 심지어 Plain-18 layer와 비교했을 때 더 빠른 수렴속도를 보여준다. 참고로 이 결과에서는 1x1 conv로 shape을 맞추지 않고 maxpooling의 stride를 2로 줘서 feature map 크기를 줄이고 증가된 차원에 대해 zero padding을 했다.

Identity vs Projection shortcuts

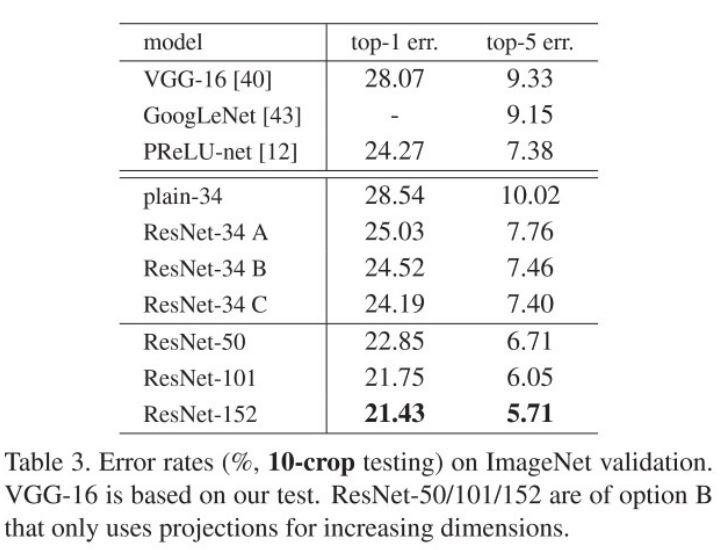
위의 표는 10-crop testing을 했을 때, 3가지에 대한 실험이다.

• A : Zero Padding (위 실험의 ResNet과 동일)
• B : feature의 dimension이 증가할 때는 Projection shortcut, 이외에는 identity shortcut
• C : 모든 shortcut에 대해 Projection shortcut

위 결과에서 B와 C는 큰 차이를 보이지 않고 A와 차이가 있는데 저자는 추가적인 parameter에 의한 성능으로 해석하고 있다. identity shortcut을 쓸 때는 parameter가 증가하지 않는 장점이 존재하기 때문에 실제 구현에서도 B가 가장 많이 쓰이고 A로 구현된 경우는 찾기가 힘들다.

나머지 50,101,152 layer들은 모두 B방식으로 구현되었다.

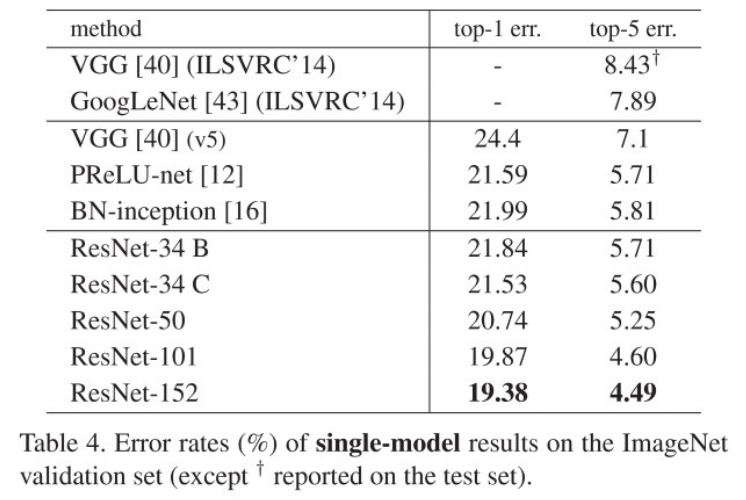
위 표는 단일 모델의 성능을 측정한 결과라고 설명이 되어있는데 GoogLeNet의 정확도를 보면 144 crop을 했을 때의 성능들을 측정한 것 같다.

ResNet-34 B만 해도 충분히 좋은 효과를 보이며 여기서 152-layer의 경우 5% 미만의 error를 보인다.

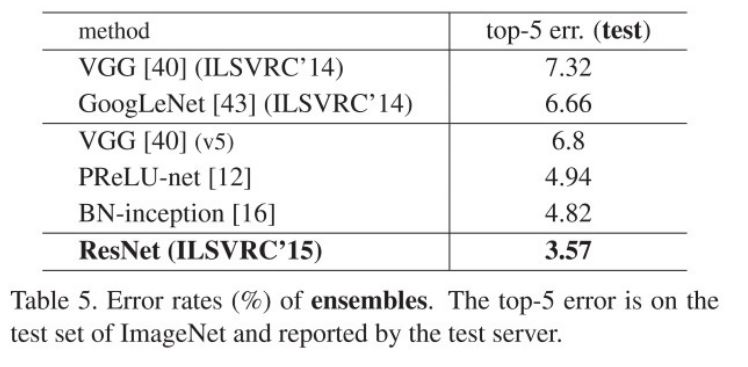
심지어 ensemble을 한 결과에서는 3.57% 까지 error를 낮출 수 있다.

CIFAR-10

CIFAR-10 dataset에서 한 실험은 오직 모델을 깊게 했을 때 어떠한 상황이 일어나는 지 관찰하는 것에 집중한다. 따라서 모델들은 zero padding shortcut (A option)을 사용한다.

convolution은 3x3 커널을 사용하고 딱 세 부분에서만 2의 stride를 주고 나머지 부분에서는 1로 shape을 유지한다. 마지막은 global average pooling과 10개의 output을 가지는 fc layer이후 softmax를 거친다.

총 layer는 6n+2로 계산한다. 예를들어 n=3인 경우 총 layer는 20이며, output map size가 32x32인 3x3 filter가 7층, 16x16인 3x3 filter가 6층, 8x8인 3x3 filter가 6층, fc layer-softmax 1층이 된다.

다른 세부사항은 다음과 같다.

• Weight Decay : 0.0001
• Momentum : 0.9
• Weight initialization : He (동일 저자)
• BN : O
• Dropout : X
• Learning rate : 0.1 이후 32k, 48k 일 때 0.1배
• iteration : 64k

아래는 실험 결과이다.

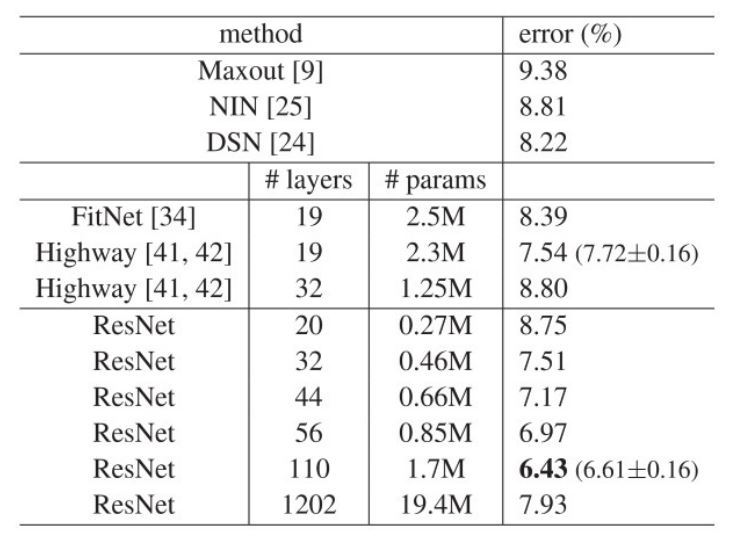
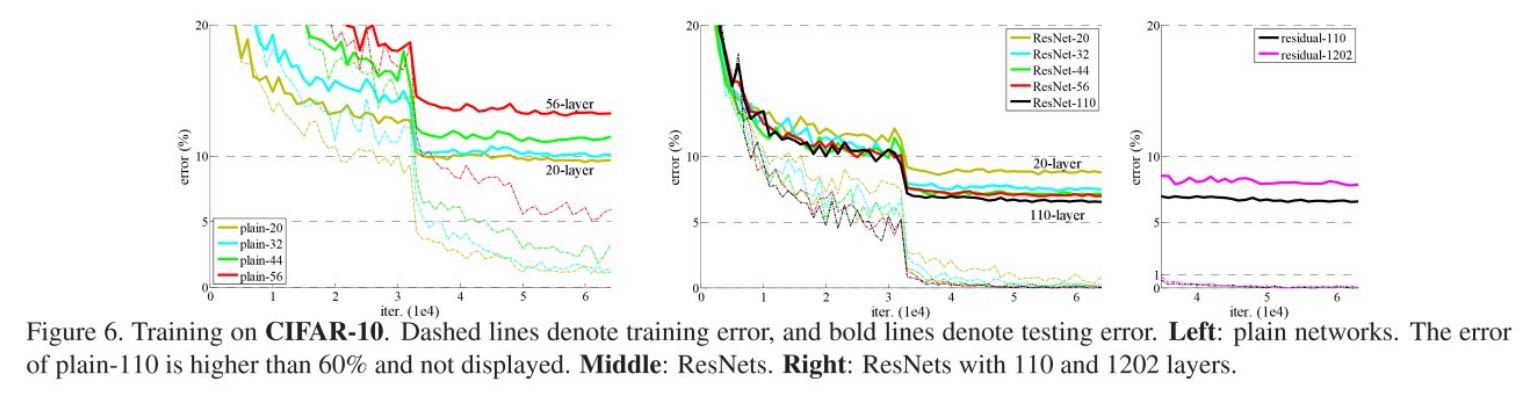
위의 그래프와 표에서는 ImageNet에서와 마찬가지로 plain network의 경우 모델이 어느정도 깊어지면 오히려 error가 올라가는 반면 ResNet에서는 줄어드는 것을 볼 수 있다. 즉, 본 논문의 내용이 ImageNet dataset에만 국한되어 있지 않다는 것이다. 1202개 까지 layer를 쌓았을 때는 오히려 32-layer보다 높은 error를 보여주는데 단순한 데이터에 비해 너무 과한 모델을 사용해 Overfitting이 발생한 것으로 주장한다.

또한 아래와 같이 Plain net과 ResNet에 대해 각각의 layer에서의 response에 대한 표준 편차를 살펴 보았다. 참고로 BN 실행이후 ReLU와 Addition 실행하기 전을 비교한 것이고 아래 그림은 표준편차를 크기별로 다시 sorting한 결과이다.

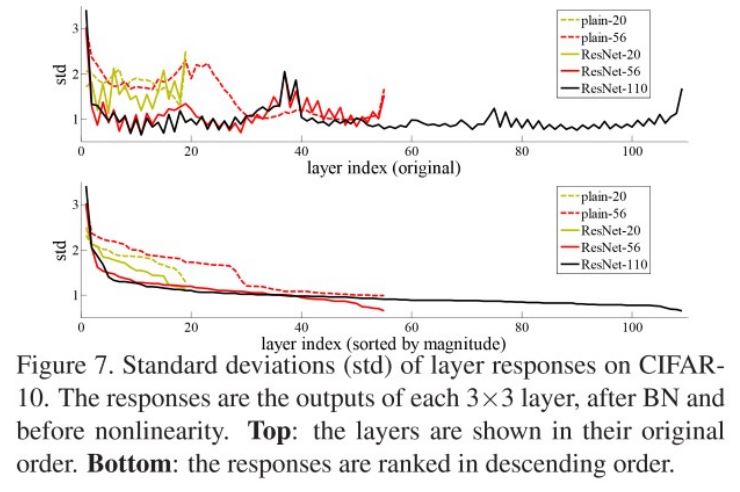
위 결과를 보면, ResNet의 결과가 더 작은 표준편차를 가지며 이로인해 Plain net에서 발생하는 문제가 ResNet에서는 적게 발생한다.

이후의 논문[2]에서 추가적인 실험을 했다. 이 논문의 요지는 원래 우리가 기대 하는 식은

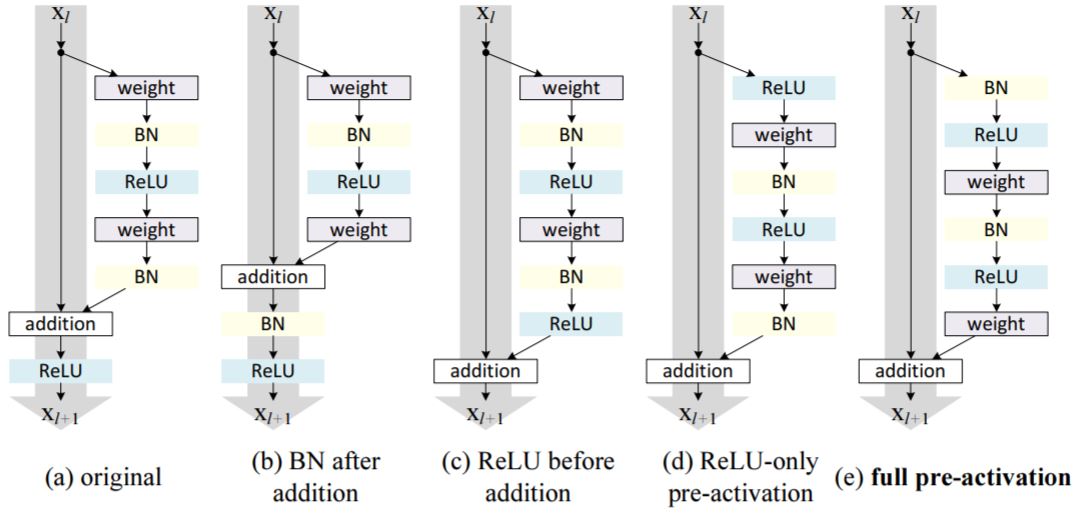
\[y = \mathcal{F}(x,\left\{ W_{i}\right\}) + x\]

인데, ReLU에 의해 Backpropagation 때 \(y = ReLU(\mathcal{F}(x,\left\{ W_{i}\right\}) + x)\) 에 대해 계산한다는 것이다. 즉, ReLu에 의해 방해를 받는 상황이 되는 것이다. 따라서 여러 실험결과(아래 사진(a)~(e)) 원래의 모델 ResNet v1(아래 사진 (a))에서 ResNet v2(아래 사진(e))의 성능이 더 좋다는 것이다.

Reference

[1] He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: CVPR., 2016.
[2] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. In ECCV, 2016.