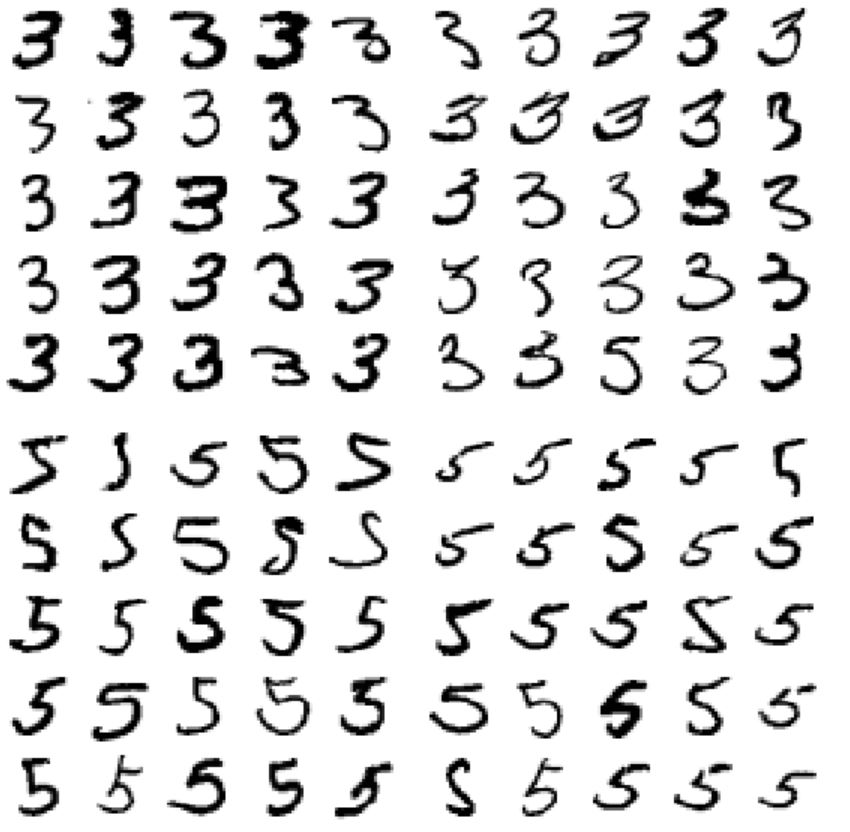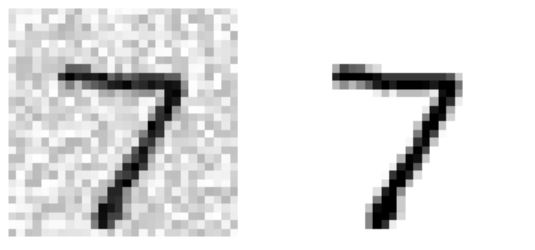15 May 2020
•
Hands On Machine Learning
선형 회귀
일반적으로 선형 모델은 입력 특성의 가중치(weight) 합과 편향(bias)이라는 상수를 더해 예측을 만든다.
\(\hat{y}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}\)
- \(\hat{y}\) : 예측값
- \(n\) : 특성의 개수
- \(x_{i}\) : \(i\)번째 특성값
- \(\theta_{j}\) : \(j\)번째 모델 파라미터 (편향 \(\theta_{0}\)과 특성의 가중치 \(\theta_{1},\theta_{2},..,\theta_{n}\) 포함).
\[\hat{y}=h_{\theta}(\mathbf{x})=\theta \cdot \mathbf{x}\]
- \(\theta\) : 편향 \(\theta_{0}\)과 \(\theta_{1}\)에서 \(\theta_{n}\)까지의 특성 가중치를 담은 모델의 파라미터 벡터.
- \(\mathbf{x}\) : \(x_{0}\)에서 \(x_{n}\)까지 담은 샘플의 특성 벡터입니다. \(x_{0}\)는 항상 1이다(편향을 미지수가 아닌 상수로 두기 위해서).
- \(\theta \cdot \mathbf{x}\) : 벡터 \(\theta\)와 \(\mathbf{x}\)의 점곱이다. 이는 \(\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}\)와 같다.
- \(h_{\theta}\)는 모델 파라미터 \(\theta\)를 사용한 가설(hypothesis) 함수이다.
모델을 훈련시킨다는 것은 모델이 훈련 세트에 가장 잘 맞도록 모델 파라미터를 설정하는 것이다. 이를 위해 먼저 모델이 훈련 데이터에 얼마나 잘 들어맞는지 측정해야 한다.
훈련 세트 \(\mathbf{X}\)에 대한 선형 회귀 가설 \(h_{0}\)의 MSE는 다음과 같이 계산한다.
\(MSE(\mathbf{X},h_{0})=\frac{1}{m}\sum^m_{i=1}(\theta^{T}\mathbf{x}^{(i)}-y^{(i)})^{2}\)
지금의 식에서는 모델이 파라미터 벡터 \(\theta\)를 가지는 것을 명확히 하려고 이렇게 표현한 것이다 이후에는 MSE(\(\theta\))로 표기된다.
1.정규방정식
비용 함수를 최소화하는 \(\theta\)값을 찾기 위한 해석적인 방법이 있다. 바로 정규 방정식(Normal equation)이다.
\(\hat{\theta}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}\)
- \(\hat{\theta}\)는 비용 함수를 최소화하는 \(\theta\) 값이다.
- \(\mathbf{y}\)는 \(y^{(1)}\)부터 \(y^{(m)}\)까지 포함하는 타겟 벡터이다.
먼저 공식을 테스트하기 위해 선형처럼 보이는 데이터를 생성하자
import numpy as np
import matplotlib.pyplot as plt
X=2*np.random.rand(100,1)
y=4+3*X+np.random.randn(100,1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()
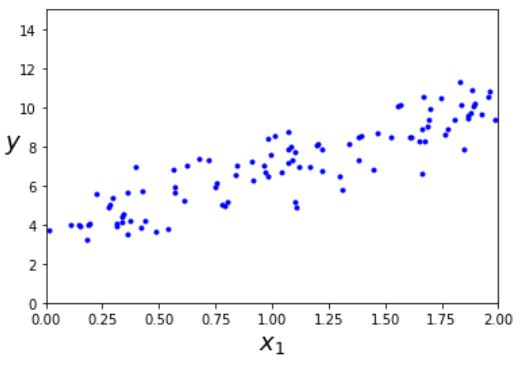
이 데이터를 생성하기 위해 사용한 함수는 \(y=4_3x_{1}+가우시안잡음\)이다. 정규방정식을 사용해 \(\hat{\theta}\)을 계산해보자. 먼저 역행렬을 계산하고 행렬곱셈을 한다.
>>> X_b = np.c_[np.ones((100,1)),X]
>>> theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
>>> theta_best
array([[3.57500712],
[3.28791026]])
rand를 써서 책과는 다른 값이 나올 수 있다. 우리는 원래의 기울기(\(x\)절편)와 편향(\(y\)절편)
이 각각 \(\theta_{0}\)=4와 \(\theta_{1}=3\)을 기대했었다. 하지만 잡음 때문에 원래 함수의 파라미터를 정확하게 재현하지는 못했다.
\(\hat{\theta}\)를 사용해 예측을 해보자. \(y_{predict} = x_{new_b} \cdot \theta_{best}\)를 한것이다.
>>> X_new = np.array([[0],[2]])
>>> X_new_b = np.c_[np.ones((2,1)),X_new]
>>> y_predict = X_new_b.dot(theta_best)
>>> y_predict
array([[ 3.57500712],
[10.15082764]])
모델의 예측을 그래프로 그리면 다음과 같다.
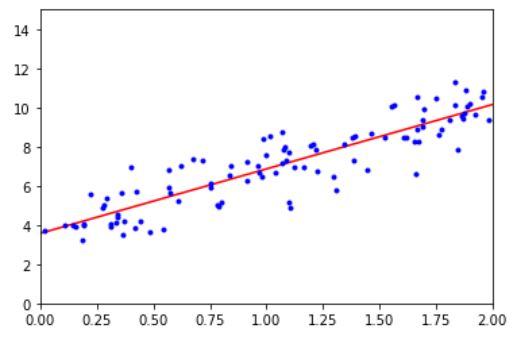
사이킷런에서는 간단하게 선형 회귀를 수행 할 수 있다.
>>> from sklearn.linear_model import LinearRegression
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X,y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([3.57500712]), array([[3.28791026]]))
>>> lin_reg.predict(X_new)
array([[ 3.57500712],
[10.15082764]])
intercept_에는 y절편(bias), coef에는 x절편(기울기)값이 들어 있다.
LinearRegression 클래스는 scipy.linalg.lstsq() 함수(‘최소 제곱(least squares)’에서 따왔다)를 기반으로 한다. 이 함수를 직접 호출할 수도 있다.
>>> theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b,y,rcond= 1e-6)
>>> theta_best_svd
array([[3.57500712],
[3.28791026]])
이 함수는 \(\hat{\theta}=\mathbf{X}^{+}\mathbf{y}\)을 계산한다. 여기서 \(\mathbf{X}^{+}\)는 \(\mathbf{X}\)의 유사역행렬(pseudoinverse, 혹은 무어-펜로즈(Moore-Penrose)역행렬)이다.
np.linalg.pinv() 함수를 사용하면 유사역행렬을 직접 구할 수 있다.
>>> np.linalg.pinv(X_b).dot(y)
array([[3.57500712],
[3.28791026]])
유사역행렬 자체는 특잇값 분해(Singular Value Decomposition, SVD)라 부르는 표준 행렬 분해 기법을 사용해 계산된다. SVD는 훈련 세트 행렬 \(\mathbf{X}\)를 3개의 행렬 곱셈 \(\mathbf{U \Sigma V^{T}}\)로 분해한다. 유사역행렬은 \(\mathbf{X^{+}=V \Sigma^{+} U^{T}}\)로 계산된다. \(\mathbf{\Sigma^{+}}\)를 계산하기 위해 알고리즘이 \(\mathbf{\Sigma}\)를 먼저 구하고 그다음 어떤 낮은 임계값보다 작은 모든 수를 0으로 바꾼다. 그 다음 0이 아닌 모든 값을 역수로 치환한다. 마지막으로 만들어진 행렬을 전치한다. 정규방정식을 계산하는 것보다 이 방식이 훨씬 효율적이다. 원래 \(\mathbf{X}\)이 특이행렬이 아닐 때 정규방정식이 작동하지 않지만 유사역행렬을 사용하면 항상 구할 수 있다.
2.계산 복잡도
정규방정식은 \((n+1) \times (n+1)\) 크기가 되는 \(\mathbf{X^{T}X}\)의 역행렬을 계산합니다. 역행렬을 계산하는 계산 복잡도(Computational complexity)는 일반적으로 \(O(n^{2.4})\)에서 \(O(n^{3})\) 사이이다. 다시 말해 특성 수가 두 배로 늘어나면 계산 시간이 대략 \(2^{2.4}=5.3\)에서 \(2^{3}=8\)배로 증가한다.
사이킷런의 LinearRegression class가 사용하는 SVD 방법은 약 \(O(n^2)\)이다. 특성의 개수가 두배로 늘어나면 계산 시간이 대략 4배가 된다.
학습된 선형 회귀 모델은 예측이 매우 빠르다. 예측 계산 복잡도는 샘플 수와 특성 수에 선형적이다. 즉 예측하려는 샘플이 두 배로 늘어나면 걸리는 시간도 거의 두 배 증가한다.
다음의 방식들은 훈련 샘플이 너무 많아 메모리에 모두 담을 수 없을 때 적합한 방식이다.
경사 하강법
경사 하강법(Gradient descent, GD)은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘이다. 경사 하강법의 기본 아이디어는 비용 함수를 최소화 하기 위해 반복해서 파라미터를 조정해가는 것이다.
경사 하강법은 기울기가 가장 가파른 방향으로 나아가는 방법이다. 파라미터 벡터 \(\theta\)에 대해 비용 함수의 현재 gradient를 계산한다. 그리고 gradient가 감소하는 방향으로 진행한다. gradient가 0이 되면 최소값에 도달한 것이다.
구체적으로 보면 \(\theta\)를 임의의 값으로 시작해서 한 번에 조금씩 비용 함수가 감소되는 방향으로 진행하여 알고리즘이 최소값에 수렴할 때까지 점진적으로 향상시킨다.
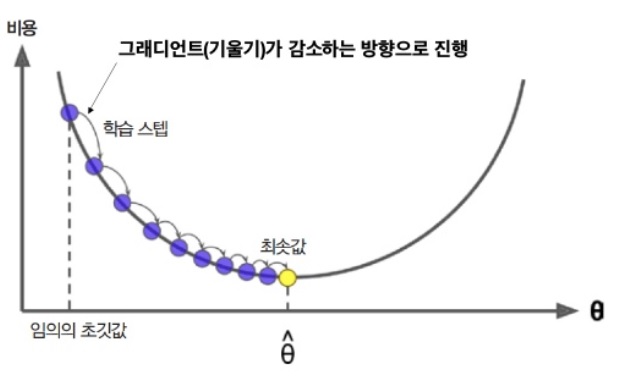
사진 출처 : 홍대 머신러닝 스터디
경사 하강법에서 중요한 파라미터는 step의 크기로, 학습률(Learning rate) 하이퍼파라미터로 결정된다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸린다.
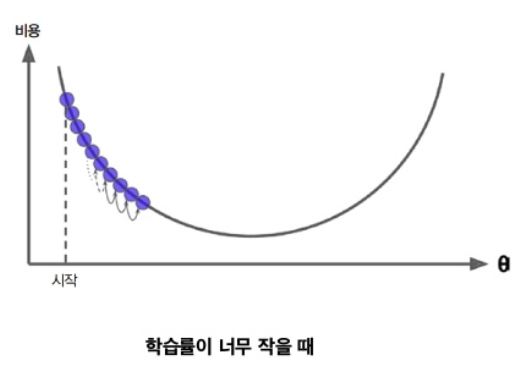
한편 학습률이 너무 크면 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 높은 곳으로 올라가게 될지도 모른다. 이는 알고리즘을 더 큰 값으로 발산하게 만들어 적절한 해법을 찾지 못하게 한다.
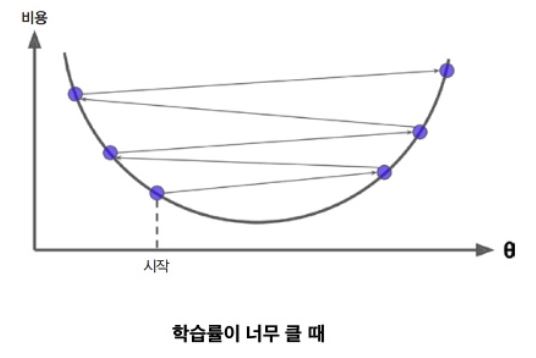
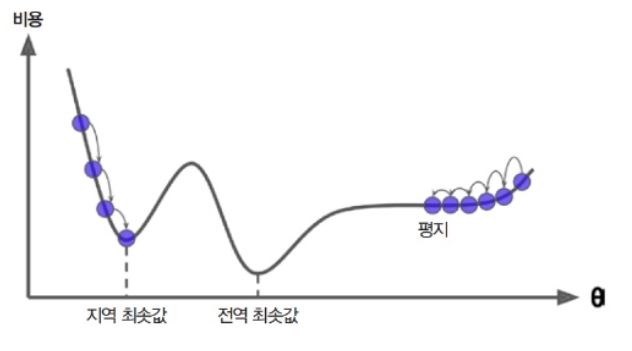
다음 그림은 2개의 문제를 보여준다.
첫째, 왼쪽에서 시작하면 경사하강법이 전역 최소값(global minimum) 보다 덜 좋은 지역 최소값(local minimum)에 수렴할 수 도 있다.
둘째, 오른쪽에서 시작하면 기울이가 0에 가까운 지역을 지나기 위해 시간이 오래 걸리고 일찍 멈추게 되어 global minima에 도달하지 못한다.
다행히 선형 회귀를 위한 MSE 비용 함수는 곡선에서 어떤 두 점을 선택해 선을 그어도 곡선을 가로지르지 않는 볼록 함수(Convex function)이다. 이는 local minima 없이 global minima만 존재 한다는 것이다. 또한 연속된 함수이고 기울기가 갑자기 변하지 않는다.
사실 특성들의 스케일이 매우 다르면 이렇게 그릇 모양이 아닌 길쭉한 모양일 수 있다.
다음 그림은 특성 1과 특성 2의 스케일이 같은 훈련 세트(왼쪽)와 특성 1이 특성 2보다 더 작은 훈련 세트(오른쪽)에 대한 경사 하강법을 보여준다.
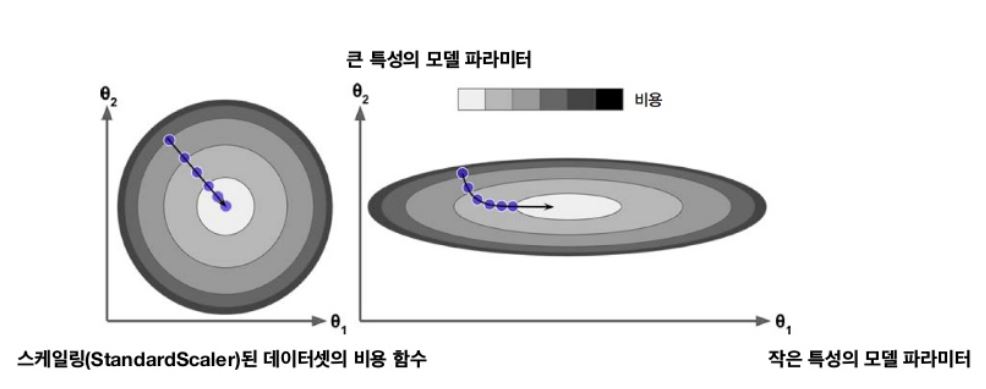
위의 사진에서 모델이 global minima에 수렴하기 위해 걸리는 시간이 다르다는 것을 알 수 있다. 그래서 경사 하강법을 사용할 때 모든 특성이 같은 스케일을 갖도록 만드는 것이 좋다. 또한, 모델 훈련이 비용함수를 최소화하는 모델 파라미터의 조합을 찾는 일인 것을 알 수 있는데 이를 모델의 파라미터 공간(Parameter space)에서 찾는다고 말한다. 모델이 가진 파라미터가 많을수록 이 공간의 차원은 커지고 검색은 더 어려워진다.
1.배치 경사 하강법
경사 하강법을 구현하려면 먼저 각 모델 파라미터 \(\theta_{j}\)에 대해 비용 함수의 gradient를 계산해야 한다. 다시 말해 모델 파라미터가 조금 변경될 때 비용 함수가 얼마나 바뀌는 지를 계산해야 한다. 이를 편도함수(Partial derivative)라고 한다. 다음 식은 파라미터 \(\theta_{j}\)에 대한 비용 함수의 편도함수 \({\partial \over \partial \theta_{j}}MSE(\theta)\)이다.
\(MSE(\mathbf{\theta})=\frac{1}{m}\sum^m_{i=1}(\theta^{T}\mathbf{x}^{(i)}-y^{(i)})^{2} \\
{\partial \over \partial \theta_{j}}MSE(\theta)=\frac{2}{m} \sum^{m}_{i=1}(\theta^{T} \mathbf{x}^{(i)}-y^{(i)})x^{(i)}_{j}\)
편도함수를 각각 계산하는 대신 다음 식을 사용하면 한꺼번에 계산할 수 있다. gradient vector \(\nabla_{\theta}MSE(\theta)\)는 비용 함수의 편도함수를 모두 담고 있다. 이 함수를 배치 경사 하강법(Batch gradient descent)라고 한다.
\[\nabla_{\theta}MSE(\theta)=\begin{pmatrix}{
\partial \over \partial \theta_{0}}MSE(\theta) \\
{\partial \over \partial \theta_{1}}MSE(\theta) \\
... \\
{\partial \over \partial \theta_{n}}MSE(\theta) \\
\end{pmatrix}=\frac{2}{m} \mathbf{X^{T} (X \theta - y)}\]
새로운 파라미터는 이 방향의 반대로 가야한다. 여기서 학습률(Learning rate) \(\eta\)가 사용된다. 내려가는 스텝의 크기를 결정하기 위해 gradient 벡터에 \(\eta\)를 곱한다.
\(\mathbf{\theta}^{(next \ step)} = \theta - \eta \nabla_{\theta}MSE(\theta)\)
이 알고리즘을 간단히 구현하면 다음과 같다.
>>> eta = 0.1
>>> n_iterations = 100
>>> m = 100
>>>
>>> theta = np.random.randn(2,1)
>>>
>>> for iteration in range(n_iterations):
>>> gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y)
>>> theta = theta - eta * gradients
>>> theta
array([[3.87460118],
[3.14424413]])
정규방정식으로 찾은 것과 정확히 같은 값이 나온다.
이번에는 leraning rate를 바꿔서 확인해 보자.
theta_path_bgd = []
def plot_gradient_descent(theta, eta, theta_path=None):
m = len(X_b)
plt.plot(X, y, "b.")
n_iterations = 1000
for iteration in range(n_iterations):
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-" if iteration > 0 else "r--"
plt.plot(X_new, y_predict, style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
plt.title(r"$\eta = {}$".format(eta), fontsize=16)
theta = np.random.randn(2,1)
plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
plt.show()
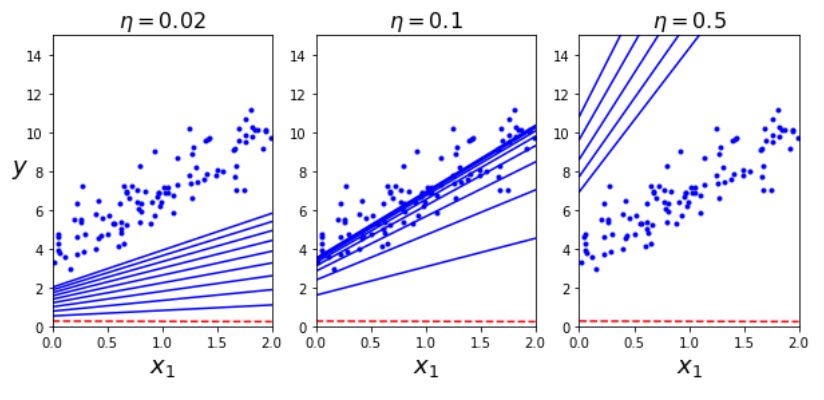
왼쪽의 학습률은 너무 낮다. 적절한 값을 내려면 아마 꽤 많은 학습시간을 소요할 것이다. 오른쪽은 학습률이 너무 높은 경우다 최적점에서 점점 더 멀어져 발산하게 되었다. 가운데가 가장 적절한 정도이다.
적절한 학습률을 찾으려면 그리드 탐색을 사용한다(2장). 하지만 그리드 탐색에서 수렴하는 데 너무 오래 걸리는 모델을 막기 위해 반복 횟수를 제한해야 한다.
여기서 반복 횟수를 지정하는 방식은 일단 횟수를 엄청 크게 하고 미리 허용오차(tolerance) \(\varepsilon\)를 지정한 후 gradient vector의 norm이 이 값 보다 작아지면 알고리즘을 종료하는 것이다.
2.확률적 경사 하강법
배치 경사 하강법의 가장 큰 문제는 매 스텝에서 전체 훈련 세트를 사용해 gradient를 계산하기 때문에 훈련 세트가 커질수록 느려지는 것이다. 이와 반대로 확률적 경사 하강법(Stochastic Gradient Descent, SGD)은 매 스텝에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 gradient를 계산한다. 한 번에 하나의 샘플을 처리하기 때문에 이전보다 더 빠르다.
반면에 확률적이기 떄문에 배치 경사 하강법보다 불안정 하다. 비용함수가 최소값에 다다를 떄까지 안정적으로 감소하지 않고 위아래로 요동치면서 평균적으로 감소한다. 시간이 지나면 최소값에 매우 근접하겠지만 요동이 지속되면서 최소값에 안착하지 못할 것이다. 알고리즘이 멈출 때의 파라미터가 최적치는 아니다.
비용 함수가 불규칙할 경우 알고리즘이 local minima 건너뛸 수 있도록 도와주므로 global minima에 접근할 확률이 늘어난다.
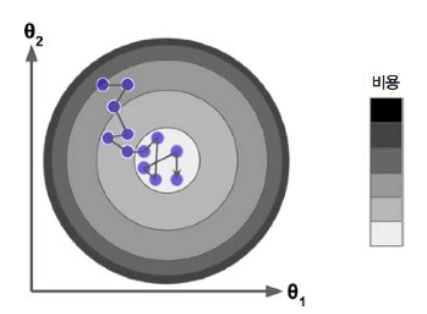
local minima에 덜 취약한 것은 좋지만 global minima에 안착하지 못한다는 점에서는 좋지 않다. 하나의 해결 방법은 학습률을 점진적으로 감소 시키는 것이다. 이 과정은 금속공학 분야에서 가열한 금속을 천천히 냉각시키는 풀림(Annealing)과정에서 영감을 얻은 담금질 기법(Simulated annealing) 알고리즘과 유사하다. 매 반복에서 학습률을 결정하는 함수를 학습 스케줄(Learning schedule)라고 부른다. 학습률에 관한 문제는 이전과 같으므로 적절한 값을 찾는게 중요하다.
다음 코드는 간단한 학습 스케줄을 사용한 SGD의 구현이다.
>>> n_epochs = 50
>>> theta_path_sgd = []
>>> m = len(X_b)
>>> t0, t1 = 5, 50 # 여기가 학습 스케줄 하이퍼파라미터
>>> def learning_schedule(t):
>>> return t0/(t+t1)
>>>
>>> theta = np.random.randn(2,1)
>>>
>>> for epoch in range(n_epochs):
>>> for i in range(m):
>>> if epoch == 0 and i < 20:
>>> y_predict = X_new_b.dot(theta)
>>> style = "b-" if i > 0 else "r--"
>>> plt.plot(X_new, y_predict, style)
>>> random_index = np.random.randint(m)
>>> xi = X_b[random_index:random_index+1]
>>> yi = y[random_index:random_index+1]
>>> gradients = 2 * xi.T.dot(xi.dot(theta)-yi)
>>> eta = learning_schedule(epoch*m+i)
>>> theta = theta - eta *gradients
>>> theta_path_sgd.append(theta)
>>> theta
array([[3.93429656],
[3.15150671]])
>>> plt.plot(X, y, "b.")
>>> plt.xlabel("$x_1$", fontsize=18)
>>> plt.ylabel("$y$", rotation=0, fontsize=18)
>>> plt.axis([0, 2, 0, 15])
>>> plt.show()
한 데이터 세트를 모두 돌았을 때를 기준으로 1에포크(epoch)라고 한다. 즉 이 코드는 전체 데이터 세트에 대해 50번 학습을 한 것이다.
다음 그림은 훈련 스텝의 첫 20개를 보여준다. step이 불규칙하게 진행하는 것을 확인할 수 있다.
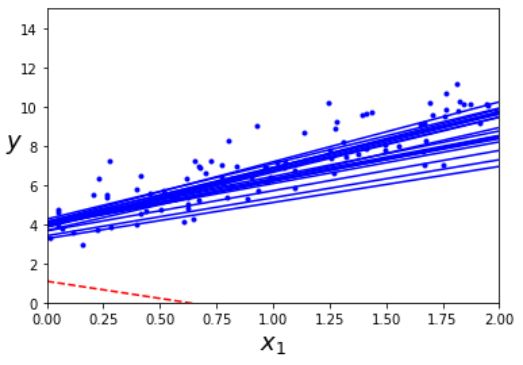
사이킷런에서 SGD 방식으로 선형 회귀를 사용하려면 기본값으로 제곱 오차 비용 함수를 최적화하는 SGDRegressor 클래스를 사용한다.
>>> from sklearn.linear_model import SGDRegressor
>>> sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
>>> ## max_iter= epoch, tol = 허용오차, penalty = 규체, eta = 학습률
>>> sgd_reg.fit(X,y.ravel())
>>> sgd_reg.intercept_,sgd_reg.coef_
(array([3.87484114]), array([3.0835934]))
3.미니배치 경사 하강법
마지막은 미니배치 경사 하강법(Mini-batch gradient descent)이다. 미니배치는 임의의 작은 샘플 세트이다. 이 작은 샘플 세트에 대해 진행함으로써 GPU와 같은 행렬 연산에 최적화된 하드웨어를 통해 성능 향상을 얻는다.
미니배치를 어느 정도 크게 하면 이 알고리즘은 파라미터 공간에서 SGD보다 덜 불규칙 하게 움직인다. SGD보다 최소값에 더 가까이 가지만 local minima에는 조금 더 민감하다.
예제는 다음과같다.
>>> theta_path_mgd = []
>>>
>>> n_iterations = 50
>>> minibatch_size = 20
>>>
>>> np.random.seed(42)
>>> theta = np.random.randn(2,1) # 랜덤 초기화
>>>
>>> t0, t1 = 200, 1000
>>> def learning_schedule(t):
>>> return t0 / (t + t1)
>>>
>>> t = 0
>>> for epoch in range(n_iterations):
>>> shuffled_indices = np.random.permutation(m)
>>> X_b_shuffled = X_b[shuffled_indices]
>>> y_shuffled = y[shuffled_indices]
>>> for i in range(0, m, minibatch_size):
>>> t += 1
>>> xi = X_b_shuffled[i:i+minibatch_size]
>>> yi = y_shuffled[i:i+minibatch_size]
>>> gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
>>> eta = learning_schedule(t)
>>> theta = theta - eta * gradients
>>> theta_path_mgd.append(theta)
>>> theta
array([[3.94654401],
[3.15293798]])
참고로 미니배치를 훈련 세트 전체로 하면 배치 경사 하강법과 똑같이 된다.
다음 그림은 세가지 경사 하강법 알고리즘이 훈련 과정 동안 파라미터 공간에서 움직인 경로이다.
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(7,4))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1, label="Stochastic")
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2, label="Mini-batch")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3, label="Batch")
plt.legend(loc="upper left", fontsize=16)
plt.xlabel(r"$\theta_0$", fontsize=20)
plt.ylabel(r"$\theta_1$ ", fontsize=20, rotation=0)
plt.axis([2.5, 4.5, 2.3, 3.9])
plt.show()
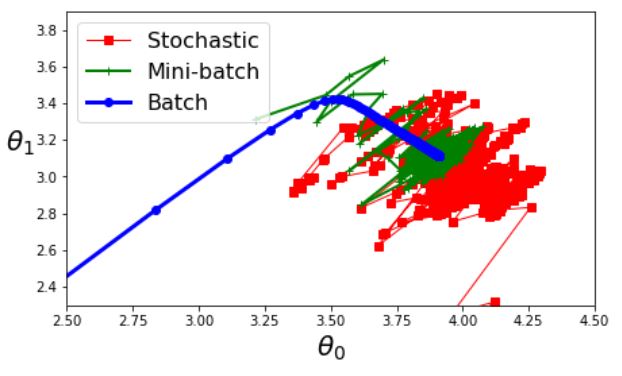
모두 최소값 근처에 도달했지만 배치 경사 하강법 빼고는 실제 최소값 근처에서 맴돈다. 하지만 배치 경사 하강법은 너무 많은 시간이 소요되고, 확률적 경사 하강법과 미니배치 경사 하강법도 적절한 학습 스케줄을 사용하면 최소값에 도달한다.
아래의 표는 지금까지 논의한 알고리즘을 선형회귀를 사용해 비교한 표이다.
| 알고리즘 |
m이 클 때 |
외부 메모리 학습 지원 |
n이 클 때 |
하이퍼 파라미터 수 |
스케일 조정 필요 |
사이킷런 |
| 정규 방정식 |
빠름 |
N |
느림 |
0 |
N |
N/A |
| SVD |
빠름 |
N |
느림 |
0 |
N |
LinearRegression |
| 배치 경사 하강법 |
느림 |
N |
빠름 |
2 |
Y |
SGDRegressor |
| 확률적 경사 하강법 |
빠름 |
Y |
빠름 |
\(\ge 2\) |
Y |
SGDRegressor |
| 미니배치 경사 하강법 |
빠름 |
Y |
빠름 |
\(\ge 2\) |
Y |
SGDRegressor |
다항 회귀
선형 모델은 비선형 데이터를 학습하는 데에도 사용할 수 있다. 간단한 방법은 각 특성의 제곱을 새로운 특성으로 추가하고, 이 확장된 특성을 포함한 데이터셋에 선형 모델을 훈련시키는 것이다. 이런 기법을 다항 회귀(Polynomial regression)라고 한다.
먼저 간단한 2차 방정식(Quadratic equation)으로 잡음이 포함된 비선형 데이터를 생성한다.
m=100
X=6*np.random.rand(m,1)-3
y=0.5*X**2+X+2+np.random.randn(m,1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()
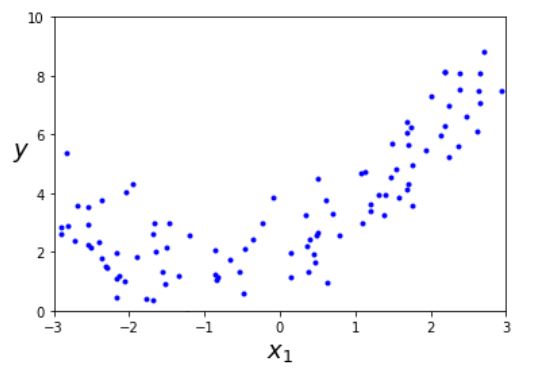
훈련 데이터의 변환은 사이킷런의 PolynomialFeatrues를 사용해 각 특성을 제곱 하여 새로운 특성을 추가할 것이다.
>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly_features = PolynomialFeatures(degree=2, include_bias=False)
>>> X_poly = poly_features.fit_transform(X)
>>> X[0]
array([2.64919746])
>>> X_poly[0]
array([2.64919746, 7.01824719])
이제 이 확장된 훈련 데이터에 Linear Regression을 적용해 보자
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X_poly,y)
>>> lin_reg.intercept_,lin_reg.coef_
(array([2.08525638]), array([[0.97095511, 0.44344077]]))
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
plt.show()
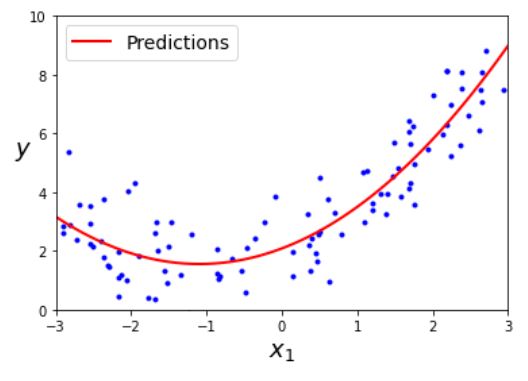
PolynomialFeatrues는 주어진 차수까지 특성 간의 모든 교차항을 추가한다.
예를들어 degree=3일 때 \(a^{2},a^{3},b^{2},b^{3},ab,a^{2}b,ab^{2}\) 모두 다 특성으로 추가한다.
14 May 2020
•
Hands On Machine Learning
MNIST
딥러닝 책을 읽어봤다면 모를 수가 없는 데이터셋이다.
먼저 MNIST 데이터세트를 다운 받아보자
>>> from sklearn.datasets import fetch_openml
>>> mnist = fetch_openml('mnist_784',version=1)
>>> mnist.keys()
dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'DESCR', 'details', 'categories', 'url'])
사이킷런에서 읽어 들인 뎅터셋들은 일반적으로 비슷한 dictionary 구조를 가지고 있다.
- 데이터셋을 설명하는 DESCR 키
- 샘플이 하나의 행, 특성이 하나의 열로 구성된 배열을 가진 data 키
- 레이블 배열을 담은 target 키
이 배열들의 shape을 확인해보자
>>> X, y = mnist["data"],mnist["target"]
>>> X.shape
(70000, 784)
>>> y.shape
(70000,)
이미지가 70,000개 있고 각 이미지에는 784개의 특성이 있다.
여기서 784개의 특성은 이미지가 28 X 28이기 때문이다. 각 featrue는 0~255까지의 값을 나타낸다.(gray scale의 픽셀 값)
그러면 이미지로 확인해보자
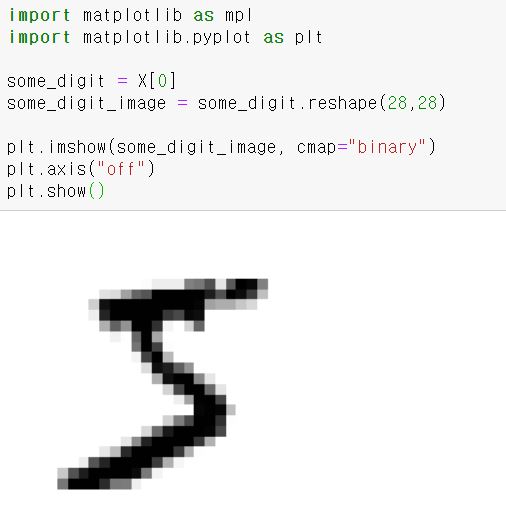
실제 레이블을 확인해보면 그림과 같이 5이다.
현재 문자열로 되어 있으므로 y를 정수형으로 변환해둬야 한다.
>>> import numpy as np
>>> y = y.astype(np.uint8)
>>> y[0]
5
위의 예제로 다운받은 MNIST 데이터 셋은 이미 train set(앞에 60000)과 test set(뒤쪽 10000)로 나눠놓아서 따로 만들 필요가 없다.
다음과 같이 미리 지정해놓으면 된다.
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
훈련세트는 이미 섞여 있어서 모든 교차 검증 폴드를 비슷하게 만든다.
어떤 알고리즘은 훈련 샘플의 순서에 민감해서 섞지 않는게 좋은 경우도 있다.
이진 분류기 훈련
문제를 단순화해서 5가 맞다 혹은 아니다 두개의 클레스를 구분할 수 있는 이진 분류기(Binary classifier)를 해보자. 분류 작업을 위해 타깃 벡터를 미리 만들어 놓자.
y_train_5 = (y_train==5)
y_test_5 = (y_test==5)
이제 분류 모델을 하나 선택해서 훈련시켜보자.
여기서는 사이킷런의 SGDClassifier 클래스를 사용해 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 분류기로 시작했다.
이 분류기는 한 번에 하나씩 훈련 샘플을 독립적으로 처리하기 때문에 매우 큰 데이터셋을 효율적으로 처리하는 장점을 지니고 있다(그래서 온라인 학습에 잘 맞다).
다음과 같이 모델을 만들고 전체 훈련 세트를 사용해 훈련하면 된다.
>>> from sklearn.linear_model import SGDClassifier
>>> sgd_clf = SGDClassifier(random_state = 42)
>>> sgd_clf.fit(X_train, y_train_5)
>>> sgd_clf.predict([some_digit])
array([ True])
fit 까지가 훈련이고 predict가 실제 test이다.
random_state는 random 함수의 seed라고 생각하면 편하다.
이제 모델의 성능을 평가해보자
성능 측정
1.교차 검증을 사용한 정확도 측정
가끔 사이킷런이 제공하는 기능보다 교차 검증 과정을 더 많이 제어해야 할 필요가 있다.
아래의 예제는 사이킷런의 cross_val_score() 함수와 거의 같은 작업을 수행하고 동일한 결과를 출력한다.
>>> from sklearn.model_selection import StratifiedKFold
>>> from sklearn.base import clone
>>>
>>> skfolds = StratifiedKFold(n_splits=3, random_state=42)
>>>
>>> for train_index, test_index in skfolds.split(X_train, y_train_5):
>>> clone_clf = clone(sgd_clf)
>>> X_train_folds = X_train[train_index]
>>> y_train_folds = y_train_5[train_index]
>>> X_test_fold = X_train[test_index]
>>> y_test_fold = y_train_5[test_index]
>>>
>>> clone_clf.fit(X_train_folds,y_train_folds)
>>> y_pred = clone_clf.predict(X_test_fold)
>>> n_correct = sum(y_pred == y_test_fold)
>>> print(n_correct/ len(y_pred))
0.95035
0.96035
0.9604
StratifiedKFold는 클래스별 비율이 유지되도록 폴드를 만들기 위해 계층적 샘플링을 수행한다.
매 반복에서 분류기 객체를 복제하여 훈련 폴드로 훈련시키고 테스트 폴드로 예측을 만든다.
그런 다음 올바른 예측의 수를 세어 정확한 예측의 비율을 출력한다.
이번에는 사이킷 런의 cross_val_score() 함수로 폴드가 3개인 k-겹 교차 검증을 사용해 SGDClassifier 모델을 평가해보자.
>>> from sklearn.model_selection import cross_val_score
>>> cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring = "accuracy")
array([0.95035, 0.96035, 0.9604 ])
두 결과가 같다는 것을 볼 수 있다.
이번에는 모든 이미지를 ‘5아님’ 클래스로 분류하는 더미 분류기를 만들어본다.
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
return self
def predict(self, X):
return np.zeros((len(X),1),dtype=bool)
모델의 정확도는 다음과 같다.
>>> never_5_clf = Never5Classifier()
>>> cross_val_score(never_5_clf,X_train,y_train_5,cv=3,scoring="accuracy")
array([0.91125, 0.90855, 0.90915])
위의 예제에서도 정확도는 90% 이상이다.
하지만 이 예제는 정확도를 분류기의 성능 측정 지표로 선호하지 않는 이유를 보여준다.
이미지의 10% 정도만 숫자 5이기 때문에 무조건 5가 아니다로 예측하면 정확히 맞출 확률이 90%이다.
특히 불균형한 데이터셋을 다룰 때 더욱 그렇다.
2.오차 행렬
분류기의 성능을 평가하는 더 좋은 방법은 오차 행렬(Confusion matrix)를 조사하는 방법이다.
기본적인 아이디어는 한 클래스의 샘플이 다른 클래스로 분류된 횟수를 세는 것이다.
테스트 세트로 예측을 만들면 안되므로 다음과 같이 cross_val_predict() 함수를 사용한다.
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
cross_val_score() 함수처럼 cross_val_predict() 함수는 k-겹 교차 검증을 수행하지만 평가 점수가 아닌 각 테스트 폴드에서 얻은 예측을 반환한다. 즉, 모델이 훈련하는 동안 보지 못했던 데이터에 대해 예측한다.
이제 confusion_matrix() 함수를 사용해 다음과 같이 오차행렬을 만들면 된다.
>>> from sklearn.metrics import confusion_matrix
>>> confusion_matrix(y_train_5,y_train_pred)
array([[53892, 687],
[ 1891, 3530]], dtype=int64)
오차 행렬의 행은 실제 클래스를, 열은 예측한 클래스를 나타낸다.
0번째 행은 5가 아닌 이미지에 대한 것이다(Negative class). 1번째 행은 5인 이미지에 대한 것이다(Positive class). 행,열 별로 다음과 같은 의미와 이름이 있다.
- (0,0) : 53,892개는 5가아니고 5아님으로 정확하게 분류했다.(true negative)
- (0,1) : 687개는 5가 아닌데 5라고 예측되었다. (false positive)
- (1,0) : 1891개는 5인데 5가 아닌 것으로 예측되었다. (false negative)
- (1,1) : 3530개는 5가 맞고 5로 정확하게 예측되었다. (true postive)
정확도가 높을 수록 대각행렬에 가까워 진다.
3.정밀도와 재현율
오차행렬이 많은 정보를 제공해주지만 가끔 더 요약된 지표가 필요할 때도 있다.
책에서는 몇가지의 지표를 설명한다.
- 양성 예측의 정확도를 분류기의 정밀도(precision)라고 한다. 분류기가 다른 모든 양성 샘플을 무시하는 것에 주의해야 한다.(5로 예측된 것중 5인 비율)
\[정밀도 = \frac{TP}{TP+FP}\]
- 분류기가 정확하게 감지한 양성 샘플의 비율로 재현율(recall), 민감도(sensitivity), 진짜 양성 비율(true positive rate, TPR) 등으로 부른다. (5인 것 중 5로 예측된 비율)
\[재현율 = \frac{TP}{TP+FN}\]
사이킷런에서는 분류기의 지표를 계싼하는 여러 함수를 제공한다.
>>> from sklearn.metrics import precision_score, recall_score
>>> precision_score(y_train_5,y_train_pred)
0.8370879772350012
>>> recall_score(y_train_5,y_train_pred)
0.6511713705958311
정밀도와 재현율을 \(F_{1}\) score라고 하는 하나의 숫자로 만들 수 있다. 특히 두 분류기를 비교할 때 유용하다.
\(F_{1}\) 점수는 정밀도와 재현율의 조화 평균(harmonic mean)이다.
\(F_{1}=\frac{2}{\frac{1}{정밀도}+\frac{1}{재현율}} = 2 \times \frac{정밀도 \times 재현율}{정밀도 + 재현율} = \frac{TP}{TP + \frac{FN+FP}{2}}\)
f1_score() 함수를 호출하면 확인 할 수 있다.
>>> from sklearn.metrics import f1_score
>>> f1_score(y_train_5,y_train_pred)
0.7325171197343846
4.정밀도/재현율 트레이드오프
정밀도와 재현율이 비슷한 분류기에서는 \(F_{1}\) 점수가 높다. 하지만 이게 항상 바람직하진 않다.
상황에 따라 정밀도가, 혹은 재현율이 더 중요할 수 있다.
예를들어, 아이들에게 안전한 동영상을 걸러내는 분류기를 훈련했을 때, 재현율은 높으나 나쁜 동영상 몇개가 노출되는 것보다 좋은 동영상이 많이 제외되더라도 안전한 것들만 노출시키는 분류기가 선회된다.
또 다른 예로, 감시 카메라를 통해 좀도둑을 잡아내는 분류기를 훈련했을 때, 분류기의 재현율이 99%라면 정밀도가 30%만 되더라도 많은 좀도둑을 잡을 수 있다.
정밀도가 올라가면 재현율은 줄고 반대도 마찬가지이다. 이를 정밀도/재현율 트레이드오프라고 한다.
SGDClassifier가 분류를 어떻게 결정하는지 보며 이 트레이드오프를 이해해보자. 이 분류기는 결정 함수(decision function)를 사용하여 각 샘플의 점수를 계산한다. 이 점수가 임계값보다 크면 샘플을 양성 클래스에 할당하고 그렇지 않으면 음성 클래스에 할당한다.
사이킷런에서 임계값을 직접 정할수는 없지만 예측에 사용한 점수는 확인할 수 있다. 분류기의 predict() method 대신 decision_function() method를 호출하면 각 샘플이 점수를 얻을 수 있다. 이 점수를 기반으로 원하는 임계값을 정해 예측을 만들 수 있다.
>>> y_scores = sgd_clf.decision_function([some_digit])
>>> y_scores
array([2164.22030239])
>>> threshold=0
>>> y_some_digit_pred = (y_scores>threshold)
array([ True])
SGDClassifier의 임계값이 0이므로 위 코드는 predict() method와 같은 결과를 반환한다. 임계값을 다음과 같이 늘리면 재현율이 줄어드는 것을 볼 수 있다.
threshold=8000
y_some_digit_pred = (y_scores>threshold)
array([ False])
이미지가 실제로 숫자 5이고 임계값이 0일 때는 분류기가 감지 했지만 임계값을 높이면 놓치게 된다.
그렇다면 어떻게 적절한 임계값을 정할 수 있을까?
이를 위해 먼저 cross_val_predict() 함수를 사용해 훈련 세트에 있는 모든 샘플의 점수를 구해야한다. 하지만 이번에는 예측결과가 아니라 결정 점수를 반환받도록 지정해야 한다.
y_scores = cross_val_predict(sgd_clf,X_train,y_train_5,cv=3,method="decision_function")
이 점수로 precision_recall_curve() 함수를 사용해 가능한 모든 임계값에 대해 정밀도와 재현율을 계산할 수 있다.
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
matplotlib을 사용해 임계값의 함수로 정밀도와 재현율을 그리는 예제는 다음과 같다.
def plot_precision_recall_vs_threshod(precisions,recalls,thresholds):
plt.plot(thresholds,precisions[:-1],"b--",label="Precision")
plt.plot(thresholds, recalls[:-1],"g-",label="Recall")
plt.legend(loc="center right", fontsize=16)
plt.xlabel("Threshold", fontsize=16)
plt.grid(True)
plt.axis([-50000, 50000, 0, 1])
recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
plot_precision_recall_vs_threshod(precisions,recalls,thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")
plt.plot([threshold_90_precision], [0.9], "ro")
plt.plot([threshold_90_precision], [recall_90_precision], "ro")
plt.show()
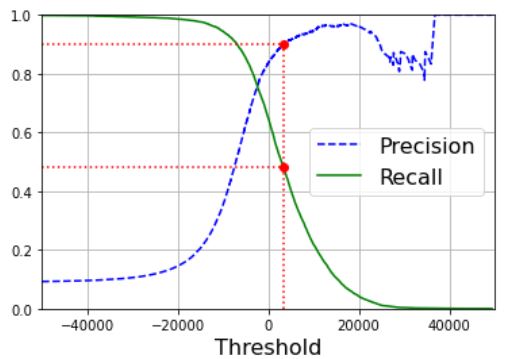
좋은 정밀도/재현율을 트레이드오프를 선택하는 다른 방법은 재현율에 대한 정밀도 곡선을 그리는 것이다.
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([0.4368, 0.4368], [0., 0.9], "r:")
plt.plot([0.0, 0.4368], [0.9, 0.9], "r:")
plt.plot([0.4368], [0.9], "ro")
plt.show()
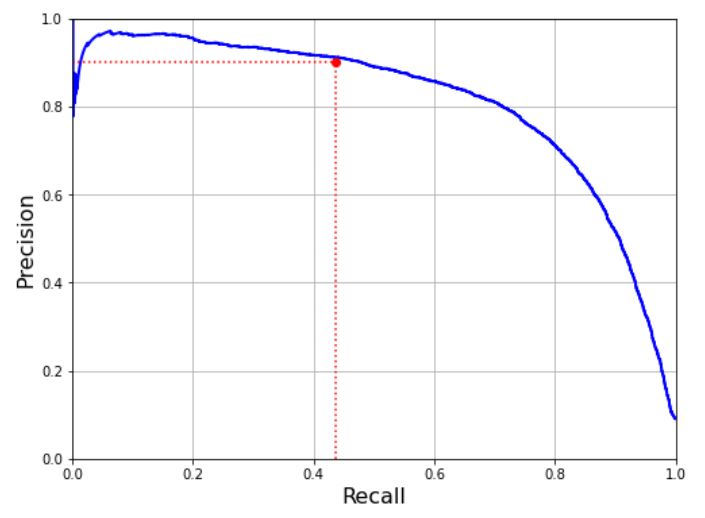
재현율 80% 근처에서 정밀도가 급격하게 줄어드는데 이 하강점 직전을 정밀도/재현율 트레이드오프로 선택하는 것이 좋다. 예를들어 재현율이 60% 정도인 지점이다. 물론 상황마다 달라진다.
정밀도 90% 달성이 목표라고 가정해보자, 그래프에서 임계값이 약 8000이라는 것을 알 수 있따. 최소한 90% 정밀도가 되는 가장 낮은 임계값을 찾을 수 있다.
threshold_90_precision = thresholds[np.argmax(precisions>=0.90)]
훈련세트에 대한 예측을 만들려면 predict() method를 호출하는 대신 y_scores에서 threshold로 하자.
y_train_pred_90 = (y_scores>=threshold_90_precision)
이 예측에 대한 정밀도와 재현율을 확인해보자
>>> precision_score(y_train_5,y_train_pred_90)
0.9000345901072293
>>> recall_score(y_train_5,y_train_pred_90)
0.4799852425751706
의도한 대로 90% 이상의 정밀도를 구할 수 있었다.
5.ROC 곡선
수신기 조작 특성(Receiver Operating Characteristic, ROC)는 곡선 이진 분류에서 널리 사용된다. 정밀도/재현율 곡선과 매우 비슷하지만, ROC 곡선은 정밀도에 대한 재현율 곡선이 아니고 거짓 양성 비율(Flase Positive Rate,FPR)에 대한 진짜 양성 비율(True Pisitive Rate,TPR,재현율)의 곡선이다.
정확하게 분류한 음성 샘플의 비율을 진짜 음성 비율(True Negative Rate, TNR)이라하고 1에서 TNR을 뺀값이 FPR과 일치한다.
TNR을 특이도(Specificity)라고도 한다. 따라서 ROC 곡선은 민감도에 대한 1-특이도 그래프이다.
3개의 약어로 표현된것들은 ~인 것중 맞춘/틀린 비율이다.
5라고 한것 중 실제 5인 비율을 나타내는 정밀도는 3개의 약어로 표현되어 있지 않다.
- \(TNR = \frac{TN}{FP+TN}\) (5가 아닌것중 5가 아니다라고 예측한 비율)
- \(FPR=\frac{FP}{FP+TN}=\frac{FP+TN-TN}{FP+TN}=1-\frac{TN}{FP+TN}=1-TNR\) (5가 아닌것중 5라고 예측한 비율)
ROC 곡선을 그리려면 먼저 roc_curve() 함수를 사용해 여러 임계값에서 TPR과 FPR을 계산해야 한다.
from sklearn.metrics import roc_curve
fpr,tpr,thresholds = roc_curve(y_train_5,y_scores)
이제 matplotlib을 사용해 TPR에 대한 FPR 곡선을 그려보자.
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16)
plt.ylabel('True Positive Rate (Recall)', fontsize=16)
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
plt.plot([4.837e-3, 4.837e-3], [0., 0.4368], "r:")
plt.plot([0.0, 4.837e-3], [0.4368, 0.4368], "r:")
plt.plot([4.837e-3], [0.4368], "ro")
plt.show()
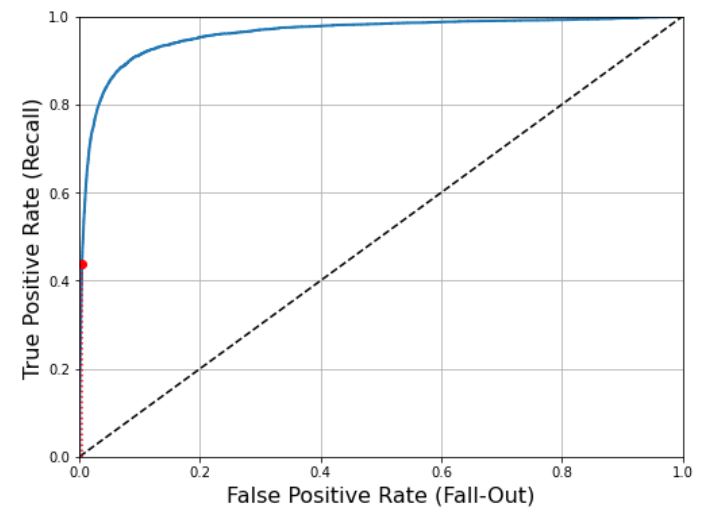
여기에서도 트레이드오프가 있다. 재현율(TPR)이 높을수록 분류기가 만드는 거짓 양성(FPR)이 늘어난다. 점선은 완전한 랜덤 분류기의 ROC 곡선을 뜻한다.
좋은 분류기는 이 점선에서 최대한 멀리 떨어져 있어야한다. (5가 아닌데 5라고 한 비율은 낮아야 하고 5인 것중 5라고 한 비율은 높아야 한다.)
곡선 아래의 면적(Area Under the Curve, AUC)을 측정하면 분류기들을 비교할 수 있다. 완벽한 분류기는 ROC의 AUC가 1이고 완전한 랜덤 분류기는 0.5이다. 사이킷런은 ROC의 AUC를 계산하는 함수를 제공한다.
>>> from sklearn.metrics import roc_auc_score
>>> roc_auc_score(y_train_5,y_scores)
0.9604938554008616
일반적으로 Positive class가 드물거나 False Negative보다 False Positive가 더 중요할 때 PR(정밀도/재현율) 곡선을 사용하고 그렇지 않으면 ROC 곡선을 사용한다. 위의 예제에서는 Negative에 비해 Positive class가 드문 경우이기 때문에 PR 곡선을 사용하는 것이 더 좋다.
RandomForestClassifier를 훈련시켜 SGDClassifier의 ROC 곡선과 ROC AUC 점수를 비교해보자.
작동방식의 차이 때문에 RandomForestClassifier에는 decision_function() method가 없기 때문에 predict_proba() method를 사용해야 한다.
predict_proba() method는 sample이 행, class가 열이고 sample이 주어진 class에 속할 확률을 담은 배열을 반환한다.(ex. 어떤 이미지가 5일 확률 70%)
>>> from sklearn.ensemble import RandomForestClassifier
>>>
>>> forest_clf = RandomForestClassifier(random_state=42)
>>> y_probas_forest = cross_val_predict(forest_clf, X_train,
y_train_5,cv=3,method="predict_proba")
[[0.11 0.89]
[0.99 0.01]
[0.96 0.04]
...
[0.02 0.98]
[0.92 0.08]
[0.94 0.06]]
roc_curve() 함수는 레이블과 점수를 기대한다. 하지만 점수 대신 클래스 확률을 전달할 수 있다. 여기서는 Positive class 확률을 점수로 사용한다.
y_scores_forest=y_probas_forest[:,1]
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
matplotlib을 사용해 그리면 다음과 같다.
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.plot([4.837e-3, 4.837e-3], [0., 0.4368], "r:")
plt.plot([0.0, 4.837e-3], [0.4368, 0.4368], "r:")
plt.plot([4.837e-3], [0.4368], "ro")
plt.plot([4.837e-3, 4.837e-3], [0., 0.9487], "r:")
plt.plot([4.837e-3], [0.9487], "ro")
plt.grid(True)
plt.legend(loc="lower right", fontsize=16)
plt.show()
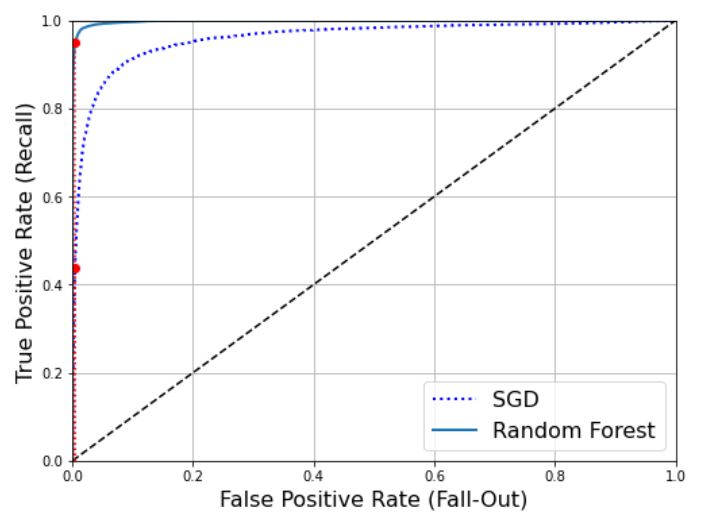
그림으로 판단하면 RandomForestClassifier의 ROC 곡선이 왼쪽 위 모서리에 더 가까워 SGDClassifier보다 훨씬 좋아 보인다. 실제로 ROC AUC 점수를 보면 다음과 같다.
>>> roc_auc_score(y_train_5,y_scores_forest)
0.9983436731328145
다중 분류
둘 이상의 클래스를 구별하는 분류기를 다중 분류기(Multiclass classifier)라고 한다.
- 이진 분류기의 종류
- 다중 분류기의 종류
- SGD 분류기, 랜덤 포레스트 분류기, 나이브 베이즈 분류기
하지만 이진 분류기를 여러 개 사용해 다중 클래스를 분류하는 기법도 있다.
OvR(One-Versus-The-Rest)(혹은 OvA(One-Versus-One))전략은 이진 분류기 여러개를 훈련시켜 이미지를 분류할 때 각 분류기의 결정 점수 중에서 가장 높은 것을 클래스로 선택한다.
또 다른 전략은 0과 1구별, 0과 2 구별, 1과 2 구별 등과 같이 각 숫자의 조합마다 이진 분류기를 훈련시키는 것이다. 이를 OvO(One-Versus-One)이라고 한다. 클래스가 N개라면 분류기는 \(N \times (N-1)/2\)개가 필요하다.(MNIST에서는 45개의 분류기를 훈련시켜야 한다는 뜻이다.)
OvO 전략의 주요 장점은 각 분류기의 훈련에 전체 훈련 세트 중 구별할 두 클래스에 해당하는 샘플만 필요하다는 것이다.
서포트 벡터 머신 같은 일부 알고리즘은 훈련 세트의 크기에 민감해 큰 훈련 세트에서 몇개의 분류기를 훈련시키는 것보다 작은 훈련 세트에서 많은 분류기를 훈련시키는 쪽이 빠르므로 OvO를 선호한다.
하지만 대부분의 이진 분류 알고리즘에서는 OvR을 선호한다.
다중 클래스 분류 작업에 이진 분류 알고리즘을 선택하면 사이킷런이 알고리즘에 따라 자동으로 OvR 또는 OvO를 실행한다. sklearn.svm.SVC 클래스를 사용해 서포트 벡터 머신 분류기를 테스트해보자.
>>> from sklearn.svm import SVC
>>> svm_clf = SVC()
>>> svm_clf.fit(X_train,y_train)
>>> svm_clf.predict([some_digit])
array([5], dtype=uint8)
내부에서는 OvO 전략을 사용해 10개의 이진 분류기를 훈련시키고 각각의 결정 점수를 얻어 점수가 가장 높은 클래스를 선택한다.
decision_function() method를 호출하면 샘플 당 10개의 점수를 반환한다. 이 점수는 클래스마다 하나씩이다.
>>> some_digit_scores = svm_clf.decision_function([some_digit])
>>> some_digit_scores
array([[ 1.72501977, 2.72809088, 7.2510018 , 8.3076379 , -0.31087254,
9.3132482 , 1.70975103, 2.76765202, 6.23049537, 4.84771048]])
값을 보면 가장 높은 점수 9.3132로 5임을 알 수 있다.
>>> np.argmax(some_digit_scores)
5
>>> svm_clf.classes_
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)
>>> svm_clf.classes_[5]
5
사이킷런에서 OvO나 OvR을 사용하도록 강제하려면 OneVsOneClassifier나 OneVsRestClassifier를 사용한다.
다음과 같이 사용하면 OvR 전략을 사용하는 다중 분류기를 만든다.
>>> from sklearn.multiclass import OneVsRestClassifier
>>> ovr_clf = OneVsRestClassifier(SVC())
>>> ovr_clf.fit(X_train,y_train)
>>> ovr_clf.predict([some_digit])
>>> len(over_clf.estimators_)
SGDClassifier(또는 RandomForestClassifier)를 훈련시키는 것도 간단하다.
>>> sgd_clf.fit(X_train, y_train)
>>> sgd_clf.predict([some_digit])
이 경우 SGD 분류기는 직접 샘플을 다중 클래스로 분류할 수 있기 때문에 별도로 사이킷런의 OvR이나 OvO를 적용할 필요가 없다. decision_function() method는 클래스마다 하나의 값을 반환한다.
>>> sgd_clf.decision_function([some_digit])
결과에서 5가 아닌 대부분의 클래스가 절대값이 큰 음수이다. 3과 5는 글씨에 따라 충분히 착각할 수 있기 때문에 양수로 나온것도 어느정도 납득이 된다.
이제 분류기를 평가해 보자. 분류기 평가에는 일반적으로 교차 검증을 사용한다. 역시 cross_val_score() 함수를 사용해 SGDClassifier의 정확도를 평가한다.
>>> cross_val_score(sgd_clf, X_train,y_train,cv=3,scoring="accuracy")
모든 test fold에서 84% 이상을 얻었다. 랜덤 분류기를 사용했다면 10%의 정확도를 얻었을 것이므로 아주 낮은 정확도는 아니지만 개선의 여지가 있다. 예를들어 간단하게 입력의 스케일으 조정하면 정확도를 더 높일 수 있다.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_tain.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
에러 분석
실제 프로젝트는 데이터 준비 단계에서 가능한 선택사항을 탐색하고, 여러 모델을 시도하고, 가장 좋은 몇 개를 골라 GridSearchCV를 사용해 하이퍼파라미터를 세밀하게 튜닝하고, 앞 장에서 한 것처럼 가능한 한 자동화한다. 이번 절에서는 가능성이 높은 모델을 하나 찾았다고 가정하고 모델의 성능을 향상시키는 방법을 찾는 절이다. 한가지 방법은 만들어진 에러의 종류를 분석하는 것이다.
먼저 오차행렬을 살펴볼 수 있다. cross_val_predict() 함수를 사용해 예측을 만들고 confusion_matrix() 함수를 호출한다.
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train,y_train_pred)
conf_mx
오차 행렬을 matplotlib의 matshow() 함수를 사용해 이미지로 표현할 수 있다.
plt.matshow(conf_max, cmap=plt.cm.gray)
plt.show()
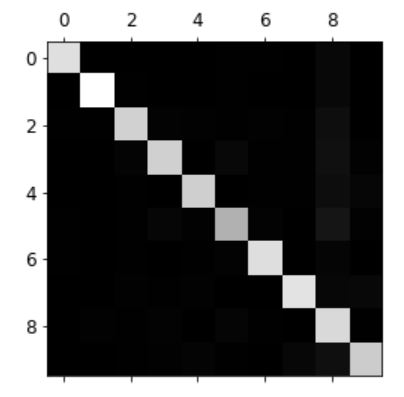
오차 행렬이 대각 행렬에 가까우므로 대부분의 이미지가 올바르게 된 것을 알 수 있다.
하지만 숫자 5의 경우 다른 숫자보다 조금 더 어둡다. 이는 데이터셋에 숫자 5의 이미지가 적거나 분류기가 숫자 5를 다른 숫자만큼 잘 분류하지 못한다는 뜻이다.
이제 에러 부분에 초점을 맞추자. 먼저 오차 행렬의 각 값을 대응되는 클래스의 이미지 개수로 나누어 에러 비율을 비교한다. 개수로 비교하면 이미지가 많은 클래스가 상대적으로 나쁘게 보이므로 이러한 방법은 피하자.
row_sums = conf_mx.sum(axis=1,keepdims=True)
norm_conf_mx = conf_mx/row_sums
다른 항목은 그대로 유지하고 주대각선만 0으로 채워서 그래프를 그려보자.
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx,cmap=plt.cm.gray)
plt.show()

사진에서 분류기가 만든 에러를 볼 수 있다. 행은 실제 클래스, 열은 예측한 클래스이다.
클래스의 8열이 상당히 밝으므로 많은 이미지가 8로 잘못 분류된 것을 확인 할 수 있따. 하지만 클래스 8의 행은 그리 낮지 않다. 이는 실제 8이 적절히 8로 분류되었다는 것을 말해준다.
여기서 확인 할 수 있듯이 오차 행렬은 반드시 대칭인 것은 아니다.
오차 행렬을 분석하면 분류기의 성능 향상 방안에 대한 통찰을 얻을 수 있다. 이 그래프를 예로 하면 8로 잘못 분류 되는것을 줄이도록 개선해야 한다. 8처럼 보이는 숫자의 훈련 데이터를 더 많이 모아서 학습하거나 동심원 같은 어떤 패턴이 드러나도록 이미지를 전처리 하는 방법도 있다.
개개의 에러를 분석해보면 분류기가 무슨 일을 하고, 왜 잘못되었는지에 대해 통찰을 얻을 수 있지만, 더 어렵고 시간이 오래 걸린다.
예를 들어 3과 5의 샘플을 그려보자.
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = mpl.cm.binary, **options)
plt.axis("off")
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()
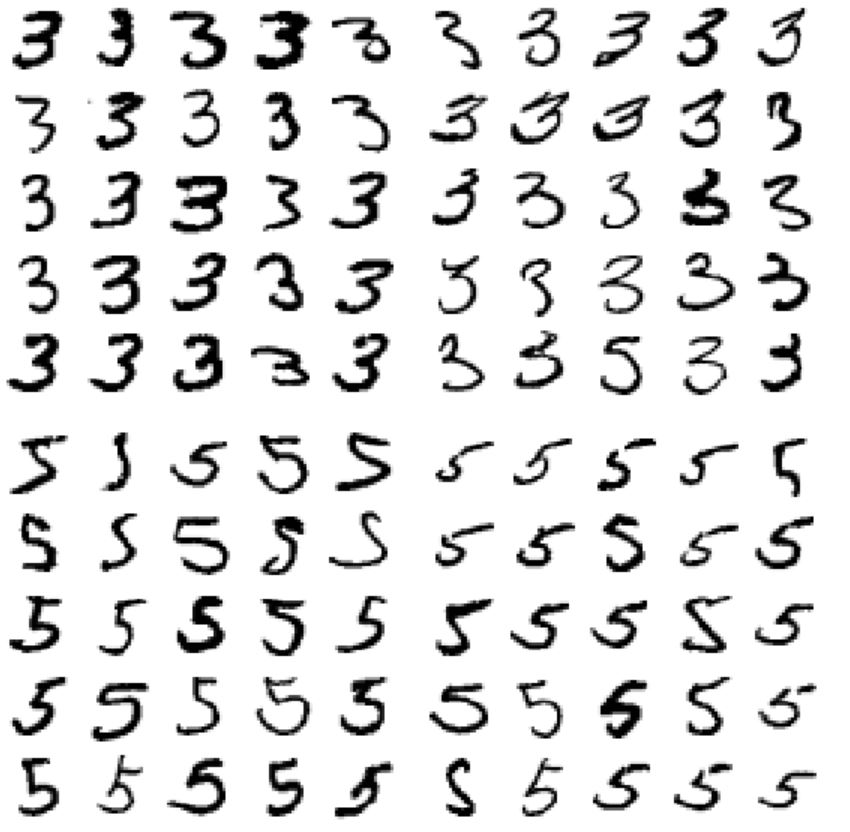
왼쪽은 3으로 분류된 이미지, 오른쪽은 5로 분류된 이미지이다. 잘못 분류된 원인은 선형 모델인 SGDClassifier를 사용했기 때문이다. 선현 분류기는 클래스마다 픽셀에 가중치를 할당하고 새로운 이미지에 대해 단순히 픽셀 강도의 가중치 합을 클래스의 점수로 계산한다. 따라서 3과 5는 몇 개의 픽셀만 다르기 때문에 모델이 쉽게 혼동한다. 따라서 3과 5는 몇 개의 픽셀만 다르기 때문에 모델이 쉽게 혼동하게 된다.
또한, 분류기는 이미지의 위치나 회전 방향에 매우 민감하다. 연결부 부위가 조금 왼쪽으로 치우치면 분류기가 5로 분류해 버린다. 에러를 줄이는 한 방법은 이미지를 중앙에 위치시키고 회전되어 있지 않도록 전처리 하는 것이다.
다중 레이블 분류
지금까지는 샘플이 하나의 클래스에만 할당되어 있지만 여러개의 클래스를 출력해야 할 때도 있다([1,0,1]식의 output). 이처럼 여러 개의 이진 꼬리표를 출력하는 분류 시스템을 다중 레이블 분류(Multilabel classification) 시스템이라고 한다.
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 ==1)
y_multilabel=np.c_[y_train_large, y_train_odd]
knn_clf = KneighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
이 코드는 각 숫자 이미지에 두 개의 타깃 레이블이 담긴 y_multilabel 배열을 만든다.
첫 번째는 숫자가 큰 값(7, 8, 9)인지 나타내고 두 번째는 홀수인지 나타냅니다. 그다음 줄이 KNeighborsClassifier 인스턴스를 만들고 다중 타깃 배열을 사용해 훈련시킨다.
이제 예측을 하면 레이블이 두 개 출력된다.
>>> knn_clf.predict([some_digit])
array([[False, True]])
올바르게 분류 되었다. 숫자 5는 7보다 작고, 홀수이다.
다중 레이블 분류기를 평가하는 방법은 많다. 지표는 프로젝트에 따라 달라진다. 예를 들어 각 레이블의 \(F_{1}\) 점수를 구하고 간단하게 평균 점수를 계산한다. 다음 코드는 모든 레이블에 대한 \(F_{1}\) 점수의 평균을 계산한다.
>>> y_train_knn_pred = cross_val_predict(knn_clf,X_train,y_multilabel,cv=3)
>>> f1_score(y_multilabel,y_train_knn_pred,average="macro")
0.976410265560605
이 코드는 모든 레이블의 가중치가 같다고 가정한 것이다.
간단한 방법은 레이블에 클래스의 지지도(Support, 타깃 레이블에 속한 샘플 수)를 주는 것이다. 이렇게 하려면 average 파라미터를 weighted로 하면 된다.
다중 레이블 분류
마지막으로 알아 볼 것은 다중 출력 다중 클래스 분류(Multioutput-multiclass classification, 혹은 Multioutput classification)이다. 다중 레이블 분류에서 한 레이블이 다중 클래스가 될 수 있도록 일반화 한것이다.
이를 위해 이미지에서 잡음을 제거하는 시스템을 만든다. 잡음이 많은 숫자 이미지를 입력으로 받고 깨끗한 숫자 이미지를 MNIST 이미지처럼 픽셀의 강도를 담은 배열로 출력한다. 분류기의 출력이 다중 레이블(픽셀당 한 레이블)이고 각 레이블은 값을 여러개 가진다(0~255).
먼저 MNIST 이미지에서 추출한 훈련 세트와 테스트 세트에 넘파이의 randint() 함수를 사용해 픽셀 강도에 잡음을 추가한다. 타겟 이미지는 원본 이미지가 된다.
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
이제 테스트 세트에서 이미지를 하나 선택한다(원래 테스트 데이터 보면 안됨).
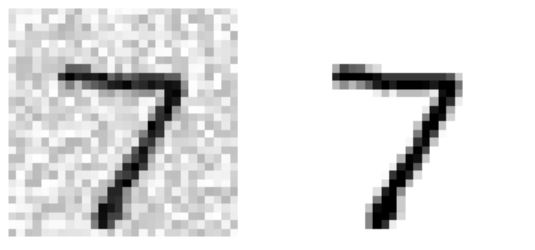
왼쪽이 잡음이 섞인 입력 이미지이고 오른쪽이 원래의 타겟이미지이다. 분류기를 훈련시켜 이 이미지를 깨끗하게 만들거다.
knn_clf.fit(X_train_mod,y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)